基本介紹
- 中文名:函式方程
- 外文名:function equation
- 含義:含有未知函式的等式
- 解法:代換法(或換元法)等
- 函式的解:能使函式方程成立的函式
- 套用學科:數學
概念
定義
解
解函式方程
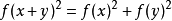
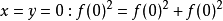
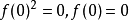
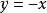

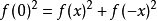
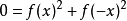
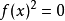
定理
解法
代換法
待定係數法
疊代法
柯西法
例子
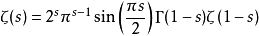
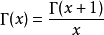
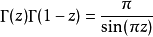

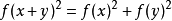
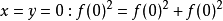
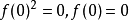
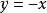

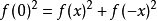
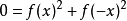
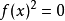
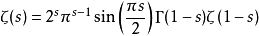
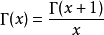
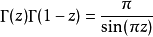
函式方程是含有未知函式的方程。函式方程可以有一個解,可以無解,也可以有多個解,甚至可以有無窮多個解。能使函式方程成立的函式叫做函式方程的解,求函式方程的解...
在數學領域,函式是一種關係,這種關係使一個集合里的每一個元素對應到另一個(可能相同的)集合里的唯一元素。...
方程(equation)是指含有未知數的等式。是表示兩個數學式(如兩個數、函式、量、運算)之間相等關係的一種等式,使等式成立的未知數的值稱為“解”或“根”。求...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
法方程是測量平差計算中的一個重要的方程,是由平差函式模型線性化後的方程式、以及在VTPV=min的條件下所導得的方程式合併而成的聯立方程組。...
薛丁格方程是量子力學最基本的方程,亦是量子力學的一個基本假定,它的正確性只能靠實驗來檢驗。薛丁格方程是量子力學的基本方程,它揭示了微觀物理世界物質運動的基本...
阿貝爾函式方程(Abel functional equation)是施洛德函式方程的一種變形方程。該方程是由阿貝爾首先提出。阿貝爾是挪威數學家。生於挪威西南海岸斯塔萬格附近的小島芬島(...
幾何方程是彈性力學中的一個描述所分析的微元體的位移與應變關係的函式方程。...... 幾何方程是彈性力學中的一個描述所分析的微元體的位移與應變關係的函式方程。...
Г函式是含參變數的以無窮乘積函式定義的反常積分。作為歐拉積分中一個重要的積分,它與B函式存在一定的聯繫。並且它在定積分也有重要的套用。...
加性函式方程(additive functional equation)是一類最簡單的函式方程,所謂加性函式方程,是指形如f(x+y)=f(x)+f(y)的方程。...
柯西方程是函式方程 f(x+y)=f(x)+f(y)此方程的解稱為加性函式...... 柯西方程是函式方程 f(x+y)=f(x)+f(y) 此方程的解稱為加性函式 ...
卡東穆塞夫-彼得韋亞斯維利方程(Kadomtsev-Petviashvili equation),簡稱KP方程,是1970年蘇聯物理學家波里斯·卡東穆塞夫 和弗拉基米爾-彼得韋亞斯維利創立以模擬非線性波動的...
使方程左右兩邊相等的未知數的值,叫做方程的解。求方程的解的過程叫做解方程。必須含有未知數等式的等式才叫方程。等式不一定是方程,方程一定是等式。...
《函式疊代與函式方程》是2010年上海科技教育出版社出版的圖書,作者是王偉葉、熊斌。本書主要是對函式疊代和函式方程的進行介紹和說明。...
施洛德函式方程(Schroderanon)一類函式方程.函式方程 _ f(B(x))=c.f(x)functional equ稱為施洛德函式方程,其中B<x)是已知函式,。是常數.如果.fi (x)是一...
包含未知函式的偏導數(或偏微分)的方程。方程中所出現未知函式偏導數的最高階數,稱為該方程的階。在數學、物理及工程技術中套用最廣泛的,是二階偏微分方程,習慣...
Lamé方程,拉梅方程的解稱為拉梅函式。...... 拉梅方程的解稱為拉梅函式。詞條標籤: 科技術語 , 科學 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版...
一般的,函式最值分為函式最小值與函式最大值。簡單來說,最小值即定義域中函式值的最小值,最大值即定義域中函式值的最大值。函式最大(小)值的幾何意義——...
三角函式是數學中屬於初等函式中的超越函式的函式。它們的本質是任何角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的。其定義...
狄拜方程式(Debye equation)也叫德拜函式*(Debye function)是彼得·狄拜(Peter Debye)於1912年估算聲子對固體的比熱的狄拜模型時創立的函式,是一類特殊函式。...
一般地,形如y=xα(α為有理數)的函式,即以底數為自變數,冪為因變數,指數...在數學分析中,三角函式也被定義為無窮級限或特定微分方程的解,允許它們的取值...
Logistic函式或Logistic曲線是一種常見的S形函式,它是皮埃爾·弗朗索瓦·韋呂勒在1844或1845年在研究它與人口增長的關係時命名的。廣義Logistic曲線可以模仿一些情況...
伽瑪函式(Gamma函式),也叫歐拉第二積分,是階乘函式在實數與複數上擴展的一類函式。該函式在分析學、機率論、偏微分方程和組合數學中有重要的套用。與之有密切聯繫...
函式的定義:給定一個數集A,對A施加對應法則f,記作f(A),得到另一數集B,也就是B=f(A)。那么這個關係式就叫函式關係式,簡稱函式。函式概念含有三個要素:定義...
拉普拉斯方程(Laplace's equation)又稱調和方程、位勢方程,是一種偏微分方程,因由法國數學家拉普拉斯首先提出而得名。拉普拉斯方程表示液面曲率與液體表面壓強之間的...
萬能公式包括三角函式、反三角函式等。萬能公式,可以把所有三角函式都化成只有tan(a/2)的多項式。將sinα、cosα、tanα代換成含有tan(α/2)的式子,這種代換稱...
一元二次方程的解:根與係數的關係主詞條:韋達定理判別式注:方程有兩個相等的實根注:方程有兩個不等的實根注:方程沒有實根,有兩個虛數數根公式三角函式公式 ...
積分是微分的逆運算,即知道了函式的導函式,反求原函式。在套用上,積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊三角形的面積,這巧妙的求解方法是積分...
