L-函式是數論中神秘而特別常見的研究對象,最簡單的例子就是Rie-mann ζ函式。類似於Riemann ζ函式,一般的L-函式也存在與之相關的廣義Riemann假設、廣義Ramanujan猜想等問題。
基本介紹
- 中文名:L類函式
- 外文名:Dirichlet L-functions
定義
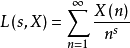

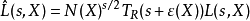
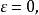

定理
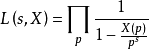
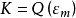

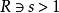
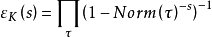
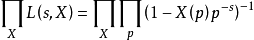
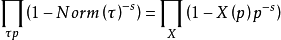


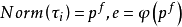
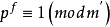
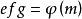
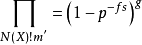
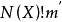
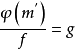


L-函式是數論中神秘而特別常見的研究對象,最簡單的例子就是Rie-mann ζ函式。類似於Riemann ζ函式,一般的L-函式也存在與之相關的廣義Riemann假設、廣義Ramanujan猜想等問題。
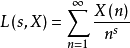

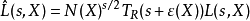
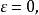

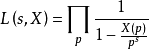
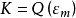

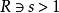
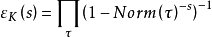
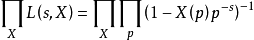
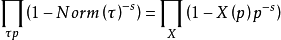


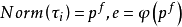
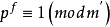
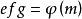
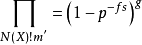
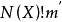
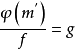

L-函式是數論中神秘而特別常見的研究對象,最簡單的例子就是Rie-mann ζ函式。類似於Riemann ζ函式,一般的L-函式也存在與之相關的廣義Riemann假設、廣義Ramanujan...
是有算術有意義和算術背景的L-函式· 例如黎曼在研究高斯和勒讓德提出的素數定理時,引出了和素數分布有關的復變數的黎曼zeta-函式。...
函式的通常形式為 Q=min{ cL,dK },其中Q是產量,L、K分別表示勞動和資本,常數c、d>0,分別為勞動和資本的生產技術係數,它們分別表示生產每一單位的產品所需要...
狄利克雷L函式,又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式。...... 又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式, 即函式,其中q≥1,Ⅹ(n)是模q的一個特...
當 介於0與1之間時,L符號為lnn的次指數(與超越多項數)函式。 [1] L符號例子 編輯 許多通用的整數分解算法都具有次指數複雜度,其中目前已知最快的為普通數域...
1916年,比伯巴赫(Bieberbach,L.)提出一個著名猜測:S類函式的冪級數展開式係數滿足|an|≤n,n=2,3,...,且僅對於克貝函式 及其旋轉等號成立,它是那樣簡單而...
該生產函式表示在既定的生產技術水平下生產要素組合(X1,X2…Xn)在每一時期所能生產的最大產量為Q。在經濟學分析中,通常只使用勞動(L)和資本(K)這兩種生產要素...
區域上處處可微分的復函式。17世紀,L.歐拉和J.leR.達朗貝爾在研究水力學時已發現平面不可壓縮流體的無旋場的勢函式Φ(x,y)與流函式Ψ(x,y)有連續的偏導數,...
L無限空間(L無限 space)亦稱本性有界函式類...... L無限空間(L無限 space)亦稱本性有界函式類.簡介在一個零集之外有界的函式的全體.若E為R”中的可測集,f...
統計學中,似然函式是一種關於統計模型參數的函式。給定輸出x時,關於參數θ的似然函式L(θ|x)(在數值上)等於給定參數θ後變數X的機率:L(θ|x)=P(X=x|θ)...
在頻譜空間中所有滿足|ξ|≤C的頻率ξ的集合稱為一個頻帶,頻譜位於這個頻帶的函式就稱為有限頻寬函式。確切地說,設f(x)∈L(R),若f(x)的傅立葉變換f^(...
的方向與目標函式的負梯度方向一致,不但如此,下面的結果表明,我們引入參數μk可以使得搜尋方向的求解更加趨於穩定,從而我們有理由相信L-M方法的數值效果應該比Gauss-...
函式環是定義在集合 L 上,取值於某數域 K 中的全體(具有某種給定性質的)函式的集合 KL ,關於函式的加法、乘法運算做成的環,稱為定義在 L 上的(具有某種性質...
o) 函式 HEX(N_or_S )函式使用說明:如果N_OR_S 是一個數字,則返回一個 十六進制值 N 的 字元串表示,在這裡, N 是一個longlong (BIGINT) 數。這相當...
hash函式1) MD4 MD4(RFC 1320)是 MIT 的Ronald L. Rivest在1990 年設計的,MD 是 Message Digest 的縮寫。它適用在32位字長的處理器上用高速軟體實現--它是...
《自守形式與L-函式簡明六章》是2012年科學出版社出版的圖書,作者是竇澤黎 張樵...... 《自守形式與L-函式簡明六章(英文版)》的主題是數論中兩個重要的課題,即...
LBound函式是Visual Basic 6.0版本所支持之函式,亦可用於VBScript,主要用於返回一個 Long 型數據,其值為指定數組維可用的最小下標...
m階L次連帶勒讓德函式(associated I_egendrefunction of order m and degree L)特殊的連帶勒讓德函式。...
《樣條函式與再生核》在樣條函式的基礎部分著重介紹了B-樣條和LB-樣條的構造...詳細研究了這類運算元樣條的性質;使得奇次樣條和自然L-樣條都成為這類運算元樣條...
getline是C++標準庫函式;但不是C標準庫函式,而是POSIX(IEEE Std 1003.1-2008...#if defined(_GNU_SOURCE) || _POSIX_C_SOURCE >= 200809L...
具體方法:給出一個關係模式R及所對應的函式依賴集F,經過初步判斷,在函式依賴集中沒有屬於L的屬性,所有屬性都是屬於LR類的,此時可以在函式依賴集中找出作為確定...
中的某個元素可以看作是所有和函式相差一個中元素的函式構成的等價類。這樣定義的空間是一個賦范向量空間,稱為S上函式關於測度μ的L空間。稱為函式的p-範數。...
在L的取法無關,則稱極限值為f(x,y)在L上對弧長的曲線積分,記為: ;其中f(x,y)叫做被積函式,L叫做積分曲線,對弧長的曲線積分也叫第一類曲線積分。(...
如果Lλ(x, λ)=c-G(x*)=0,那么說明資源全部被使用,其邊際效用λ>0。注意:這裡我們通過對拉格朗日乘數的解釋考查了cj的微小變動dcj對目標函式最大值的變化...
