設D是Rn中的一個區域,f:D→Rn是以D為定義域的映射,如果f在D上的每一點處可微,則稱f為D上的可微映射。
基本介紹
- 中文名:可微映射
- 外文名:differentiable map
- 所屬學科:數學(微分拓撲學)
- 相關概念:可微,連續映射等
連續映射

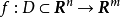
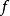
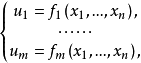
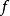
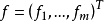
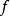


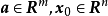
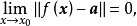
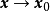
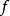

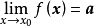
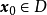
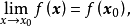
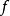
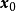
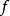
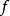
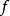

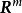
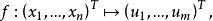
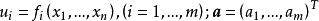
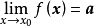
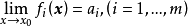
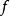
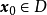

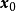
可微映射


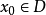
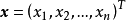




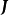


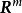


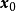
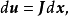
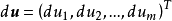
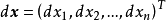
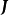


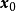
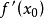
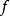
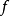
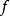

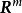
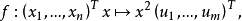
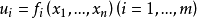
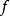
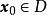
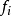
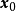
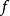
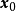
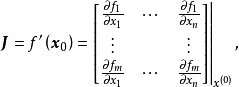
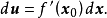
複合映射求導的鏈式法則

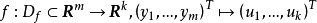
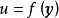
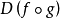
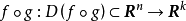
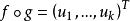
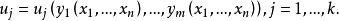
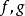
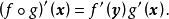
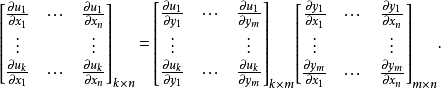

設D是Rn中的一個區域,f:D→Rn是以D為定義域的映射,如果f在D上的每一點處可微,則稱f為D上的可微映射。

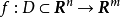
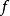
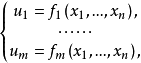
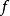
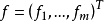
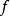


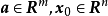
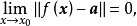
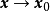
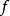

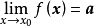
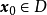
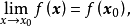
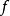
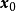
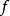
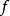
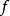

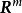
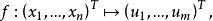
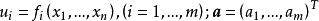
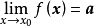
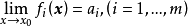
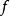
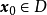

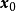


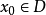
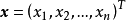




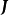


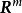


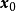
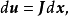
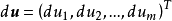
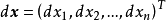
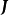


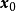
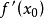
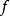
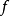
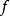

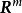
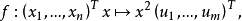
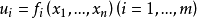
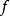
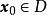
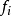
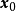
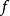
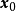
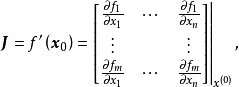
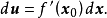
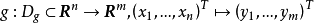

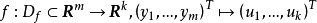
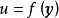
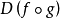
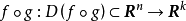
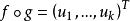
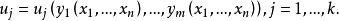
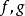
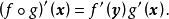
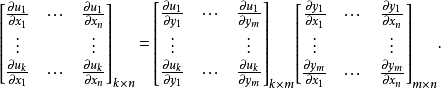
設D是Rn中的一個區域,f:D→Rn是以D為定義域的映射,如果f在D上的每一點處可微,則稱f為D上的可微映射。...
安諾索夫可微映射(Anosov differentiablemap)是比安諾索夫微分同胚和擴張映射更廣的一類。...
可微映射的奇點理論,一門年輕的數學分支,也是現代數學中得到蓬勃發展的領域之一。...... 可微映射的奇點理論,一門年輕的數學分支,也是現代數學中得到蓬勃發展的領域...
可微映射穩定性(stability of differentiablemapping)反映一個映射經小擾動後本質不變的特性.設M,N是兩個微分流形,f,g;M}N是兩個無窮次可微映射,若存在無窮次...
可微映射無窮小穩定性(infinitesimal stabil-ity of differentiable mappings)利用切空間給出的一種關於映射的穩定性概念,其優點是可以計算且在一定條件下與通常穩定性...
可微映射秩(rank of differentiable map)是對可微映射的一種刻畫。...... 可微映射秩[1] (rank of differentiable map)是對可微映射的一種刻畫。...
切映射是一種可微映射。微分流形之間的可微映射誘導出它們的切叢之間可微映射。...... 切映射是一種可微映射。微分流形之間的可微映射誘導出它們的切叢之間可...
度量空間亦稱距離空間。一種拓撲空間,其上的拓撲由距離決定。可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,f:M→M是一連續映射,如果...
可微函式芽環(ring of germs of differentiablefunctions)是一種特殊的環。指可微函式芽的全體在以自然方式定義的加法、乘法下構成的環。考慮n維歐氏空間R上的無窮...
精確地(Rudin 1973, 定理2.11):如果X和Y是巴拿赫空間,A : X→ Y是一個滿射的連續線性運算元,那么A就是一個開映射(也就是說,如果U是X內的開集,那么A(U)...
可微奇異p單形(differentiable singular p-simplex)是單形到流形的一種映射。...... 可微奇異p單形(differentiable singular p-simplex)是單形到流形的一種映射...
微分流形之間的一類同胚映射。它與它的逆映射都是可微的。設M,N均為微分流形,對於映射f:M→N,若f是同胚映射,並且f,f-1都是Cr可微映射,則稱f為M到N上...
映射在一點處微分(differential of map at apoint)亦稱映射在一點處的切映射一種特殊的映射.由微分流形之間的可微映射誘導出的它們切空間之間的一種線性映射.若...
映射正則點(regular point of map)微分流形上一類特殊的點.指微分流形上的那種點,可微映射在該點處是淹沒映射。...
浸入亦稱浸入映射,是具有某種性質的流形間的映射。設𝜙:M→N是一個可微映射,若對於每個p∈M,𝜙∗|p為非奇異的,則稱𝜙為浸入映射,簡稱浸入。...
流形嵌入(embedding of manifold)是指一類特殊的可微映射,它把一個流形微分同胚地映射到另一個流形的子流形上。...
設φ是從C流形M到C流形N的連續映射,如果對於N上的任意Cr函式ƒ,M上的函式ƒ。φ總是Cr的,則稱φ是Cr可微映射,或簡稱Cr映射。如果φ是從M到N上的同胚...
