偽阿諾索夫映射

偽阿諾索夫（Аносов）映射是曲面的一種同胚或微分同胚，是環面上的線性阿諾索夫微分同胚的推廣。

映射是數學分析的基本概念及研究對象。映射與函式(還有變換、運算元等)同樣指集合之間的對應關係，是同一數學概念在不同數學分支及其不同發展過程中使用的不同稱呼，現仍保留在各數學分支中。

基本介紹

• 中文名：偽阿諾索夫映射
• 外文名：Аносов map
• 屬性：曲面的一種同胚或微分同胚
• 相關人物：威廉·瑟斯頓
• 領域：數學
• 空間：環面

概念

偽阿諾索夫（Аносов）映射是曲面的一種同胚或微分同胚，是環面上的線性阿諾索夫微分同胚的推廣。偽阿諾索夫映射的定義用到威廉·瑟斯頓提出的測度葉狀結構概念。“偽阿諾索夫映射”這一名詞，也是他證明曲面的微分同胚分類時所創。

映射

設A，B是兩個非空集合。如果A中的每 一個元素，依據 一個確定的關係f，在B中都有一個且僅有一個元素與它對應，那么就把這種對應關係稱為集合A到集合B的映射。記作f：A→B。其中，集合A稱為映射的定義域，A中的每一個元素α稱為原像；在映射f 下，元素α與B中的元素b對應，稱b為元素α在映射f下的像，記作b=f(α)；全體像的集合，稱為映射f的值域，記作f(A)。顯然，f(A)⫅B：當f(A)⊂B時，我們稱f為集合A到集合B內的映射；當f(A)=B時，我們稱f為集合A到集合B上的映射。

同胚

同胚是拓撲空間之間的一種變換。若f是拓撲空間(X，T)到(Y，U)的單滿映射，並且f與f都是連續的，則稱f為同胚映射或拓撲變換。存在同胚映射的兩個拓撲空間稱為同胚的或拓撲等價的。同胚關係是等價關係。抽象空間的同胚是弗雷歇(M.-R.Fréchet)於1910年開始研究的。在狹窄的意義下同胚的概念早已被龐加萊((J.-)H.Poincaré)引入。

設E與F為兩個拓撲空間。稱從E到F上的雙射為從E到F上的同胚，如果這一映射能建立一個從E之全體開集的集合到F之全體開集的集合上的雙射。

為使從E到F上的雙射是同胚，其充分必要條件是： 這個雙射是雙連續的。

從一緊空間到另一緊空間上的任一連續雙射是同胚。

微分同胚

微分流形之間的一類同胚映射。它與它的逆映射都是可微的。設M，N均為微分流形，對於映射f：M→N，若f是同胚映射，並且f，f^-1都是C^r可微映射，則稱f為M到N上的C^r微分同胚。C^∞微分同胚f：M→N簡稱M到N上的微分同胚。對於微分流形M，N，若存在(C^r)微分同胚f：M→N，則稱M與N是(C^r)微分同胚的微分流形，記為M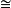N。“”是微分拓撲學中的基本等價關係。微分拓撲的基本任務是研究微分流形在微分同胚下保持不變的性質，以及尋求在怎樣的條件下兩個微分流形是微分同胚的。米爾諾(J.W.Milnor)於1956年證明，在S⁷上至少存在兩個不微分同胚的微分構造。後來證實，S⁷上恰好有15個這樣的不同的微分構造。

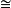
環面

一類特殊的對稱空間。若G是一個連通李群，則G×G也是連通李群，並有對合自同構σ：σ(g₁，g₂)=(g₂，g₁)，(g₁，g₂)∈G×G.σ的特徵子群ΔG={(g，g)∈G×G|g∈G}與G同構，稱為對角子群。作為微分流形，G×G/ΔG與G是同胚的。特別地，G為連通緊李群時，G×G/ΔG是黎曼對稱空間。G為連通緊交換李群時，G×G/ΔG(同胚於G)為環面，是黎曼對稱空間，其對應的正交對稱李代數是歐幾里得型的。

代數群的一個重要子群。指與n階可逆對角矩陣全體所成的群D(n，K)同構的代數群。環面的有理表示都是完全可約的，不可約表示都是一維的。所以環面的表示理論被特徵標群完全刻畫。一個代數群中的極大環面子群(簡稱極大環面)在這個代數群的結構與表示理論中起著至關重要的作用。不同的極大環面在代數群中是互相共軛的。