在數學中,微分同胚是適用於微分流形範疇的同構概念。這是從微分流形之間的可逆映射,使得此映射及其逆映射均為光滑(即無窮可微)的。
基本介紹
- 中文名:微分同胚
- 外文名:diffeomorphism
- 簡稱:微分同胚
- 適用:適用於微分流形範疇的同構概念
- 相關術語:微分流形
- 套用學科:數學
定義

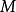

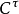
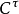
例子
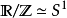
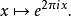
與同胚的關係


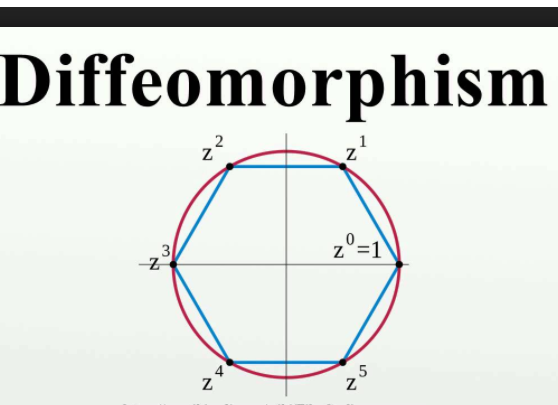
在數學中,微分同胚是適用於微分流形範疇的同構概念。這是從微分流形之間的可逆映射,使得此映射及其逆映射均為光滑(即無窮可微)的。

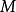

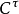
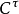
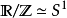
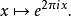


在數學中,微分同胚是適用於微分流形範疇的同構概念。這是從微分流形之間的可逆映射,使得此映射及其逆映射均為光滑(即無窮可微)的。...
設M,N分別是兩個Ck流形,映射f:M→N是一個雙射,使得f與f-1是Ck映射,則稱f為M與N之間的Ck微分同胚。...
類梯度微分同胚(gradient - like diffeomor -phism)是莫爾斯一斯梅爾微分同胚的著名特例。...
單參數微分同胚群(one parameter group of diffeomorphisms)是含一個參數的微分同胚全體構成的群。...
在拓撲學中,同胚(homeomorphism、topological isomorphism、bi continuous function)是兩個拓撲空間之間的雙連續函式。同胚是拓撲空間範疇中的同構。...
研究微分流形和可微映射的一個數學分支。微分流形除了是拓撲流形外,還有一個微分結構。因此,對於從一個微分流形到另一個微分流形的映射,不僅可以談論它是否為...
緊緻曲面微分同胚分類(differentially home-omorphic classification of compact surfaces)拓撲學(包括代數拓撲學、微分拓撲學)中的一個著名結果.這種完整的拓撲分類定理...
微分拓撲學是研究微分流形在微分同胚映射下不變的性質的數學分支。研究的基本對象是微分流形或帶邊的微分流形以及這樣的流形之間的可微映射。...
在數學中,一個辛同胚(symplectomorphism)是辛流形範疇中的一個同構。...... 是一個辛同胚如果它是一個微分同胚且 ω2在f下的拉回等於 ω1:辛同胚的...
微分流形(differentiable manifold),也稱為光滑流形(smooth manifold),是拓撲學和幾何學中一類重要的空間,是帶有微分結構的拓撲流形。 微分流形是微分幾何與微分...
微分拓撲法是研究微分流形和可微映射的一種拓撲學方法。美國數學家惠特尼(H.Whitney)是微分拓撲法的奠基人,在1936年他就得到了浸入定理。凱恩斯和懷特海也進行了有...
系統科學的一個數學分支。主要研究隨時間演變的動力系統的整體性質及其在擾動中的變化。微分動力系統的研究始於20世紀60年代初,其前身為常微分方程定性理論和動力系統...
微分動態系統(differential dynamic system) 現代數學的新興分支之一微分動態系統是研究微分流形上連續或離散的可微分動態系統軌道整體 (大範圍)性質的新興數學分支...
《微分幾何與拓撲學簡明教程》是2006年高等教育出版社出版的圖書,作者是(俄羅斯)米先柯。本書適合數學、物理及相關專業的高年級本科生、研究生、高校教師和研究人員...
微分同胚共變性為物理定律的形式在任意微分坐標轉換下保持不變。...... 微分同胚共變性為物理定律的形式在任意微分坐標轉換下保持不變。其精神在於坐標並非先驗地存在...
一維流形微分同胚分類(differentially home-omorphic classification of 1-Manifolds)流形關於微分同胚的分類問題的一個重要結果.作為莫爾斯函式在流形分類上的簡單套用...
微分流形定向(orientation of differentialmani-fold)具有定向性質的微分流形.設M是n維微分流形,M是可定向的若且唯若存在M的(光滑)圖冊中,適合:b (U,卯,(V,...
映射在一點處微分(differential of map at apoint)亦稱映射在一點處的切映射一種特殊的映射.由微分流形之間的可微映射誘導出的它們切空間之間的一種線性映射.若...
完全類似地可給出莫爾斯-斯梅爾微分同胚的定義。動力系統理論已經證明:任何緊緻微分流形上都存在莫爾斯-斯梅爾系統,這個重要事實是由莫爾斯(H.M.Morse)及斯梅爾(S....
偽阿諾索夫(Аносов)映射是曲面的一種同胚或微分同胚,是環面上的線性阿諾索夫微分同胚的推廣。映射是數學分析的基本概念及研究對象。映射與函式(還有變換、...
光滑映射在一點穩定性(stability of asmooth mapping at a point)是指光滑映射在一點局部經小擾動後本質不變的特性。光滑映射是一類連續映射,是微分拓撲學的基本...
子流形管狀鄰域(tubular neighborhood ofsubmanifold)是微分拓撲中的一個工具。利用管狀鄰域的存在性和橫截性定理,可以證明惠特尼定理:任何(無邊)緊緻微分流形微分...
平凡切叢(trivial tangent bundle)一類特殊的切叢.判斷一個微分流形的切叢是否平凡的,這是微分拓撲學的重要問題之一設M是n維微分流形,對於M的切叢TM,若存在...
ζ 函式(ζ-function)是用來刻畫系統周期點性態的函式,是動力微分系統的重要研究對象。Smale猜測公理A微分同胚有有理的ζ函式,以後Maninng使用Markov分解這一手段...
1 概念 2 度量空間 3 連續映射 4 同胚的概念 5 微分同胚 可擴映射概念 編輯 可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,...
