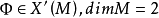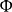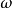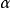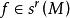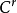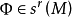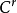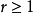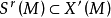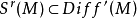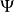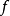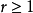莫爾斯-斯梅爾系統(Morse-Smale system)是最早得到的一類結構穩定系統。這類系統有一特性:它的非遊蕩集僅由有限個數的周期元素組成,對這類系統的研究是從1937年獲得的龐特里亞金-安德羅諾夫定理的結論開始的,它的通常定義如下:設M是緊緻黎曼流形,X是M上的Cr向量場,如果:1.X有有限個奇點和周期軌道,它們都是雙曲的;2.若σ1和σ2是X的奇點或周期軌道,那么σ1與σ2的穩定流形與不穩定流形是橫截相交的;3.非遊蕩集Ω(X)恰是X的奇點和周期軌道,則稱X是莫爾斯-斯梅爾向量場。完全類似地可給出莫爾斯-斯梅爾微分同胚的定義。動力系統理論已經證明:任何緊緻微分流形上都存在莫爾斯-斯梅爾系統,這個重要事實是由莫爾斯(H.M.Morse)及斯梅爾(S.Smale)得到的,故這一類系統通常就以他們的名字命名。
基本介紹
- 中文名:莫爾斯-斯梅爾系統
- 外文名:Morse-Smale system
- 所屬學科:數學
- 所屬問題:動力系統(微分動力系統)
定義
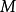
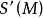
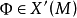
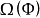
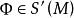
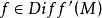
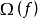
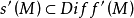
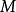

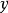
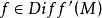
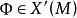
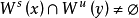

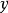
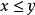
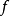
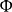
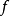
相關定理