基本介紹
- 中文名:可定向流形
- 外文名:orientable manifold
- 所屬學科:數學
- 所屬領域:幾何拓撲學
基本介紹


























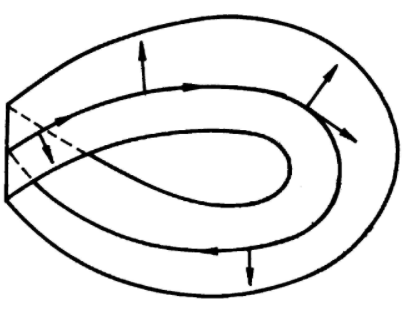 如圖1
如圖1相關性質定理
























































 如圖1
如圖1




























如果可找到一些局部參變數表示fi確定M的一個定向(如上所述),就說M是可定向的,一個流形M,即令是連通的,並不總是可定向的:“默比烏斯帶”提供了不可定向曲面...
拓撲流形定向確定流形指向的方式問題.有多種等價的方式來定義流形的定向.這裡介紹比較基本的兩種.設M為n維拓撲流形。...
微分流形定向(orientation of differentialmani-fold)具有定向性質的微分流形.設M是n維微分流形,M是可定向的若且唯若存在M的(光滑)圖冊中,適合:b (U,卯,(V,...
《流形上的分析》可作為數學專業的研究生和高年級本科生的教材或參考書,也可供物理及某些工科專業的研究生、青年教師和有關工程技術人員參考。...
積分流形(integral manifold)是一類子流形。它是由對合分布確定的子流形。流形是一類拓撲空間,它在每一點的附近都與歐氏空間同胚。一般的流形概念,起始於對於可...
如果可選取坐標圖冊使微分流形M中各個坐標鄰域之間的坐標變換的雅可比行列式都大於零,則稱這個流形是可定向的。球面是可定向的,麥比烏斯帶是不可定向的。...
dianalytic流形是復解析流形的推廣,有可能是不可定向的。流形的dianalytic結構由圖卡所組成的圖冊給出,而圖卡間的轉移映射,可以是復解析映射,或復解析映射的復...
當然,瑟斯頓也注意到在閉3維流形的非平凡連通和之中,除了RP3 # RP3以外,均無上述意義下的幾何,因此他的工作中也包含一些幾何猜想,即他認為任何緊緻、可定向3...
保定向映射(orientation preserving map)指保持兩個流形確定定向的映射。...... 保定向映射指保持兩個流形確定定向的映射。設M, N是兩個可定向的n維流形,映射ψ...
定向配邊類(oriented cobordism class)是流形的一種等價類,對於兩個光滑緊定向n維流形M與M′,若存在一個光滑緊的帶邊的定向流形X,使得∂X及其誘導定向在保持...
設M為緊緻單連通的4維拓撲流形,s,s'為M中可定向閉曲面,它們處於一般位置,因為(M>1,M為可定向流形,交點數1.(S,S')隨S(或s')的改變定向而改變符號,...
設M是緊可定向流形,E,F是M上的C∞復向量叢,線性映射P:C∞(E)→C∞(F),其中C∞(E)與C∞(F)分別是E與F的C∞截面構成的復向量空間,若在局部坐標下P...
不可壓縮曲面在3維流形的研究中起著重要的作用.有如下定理:若M為緊緻3維流形,}M中的每個分支在M中不可壓縮,群的自由積,則關於不可定向流形,衣潑斯坦((...
《微分流形初步》是2002年高等教育出版社出版的圖書,作者是陳維桓。...... 《微分流形初步》是2002年高等教育出版社...可定向微分流形和帶邊流形 1°流形的...
注意,若M,N不是可定向流形,f:M→N為連續映射,則取與f同倫的C映射h:M→N,對於h的正則值q∈N,記deg2(h,q)為h(q)M中點的個數的模2剩餘類,它與h...
克萊因瓶是一個不可定向的二維緊流形,而球面或輪胎面是可 克萊因瓶 定向的二維緊流形。如果觀察克萊因瓶,有一點似乎令人困惑--克萊因瓶的瓶頸和瓶身是相交的...
令 M 為一個可定向分段光滑 n 維流形,令 ω 為 M 上的 n−1 階 C 類緊支撐微分形式 [2] 。如果 ∂M 表示 M...
莫比烏斯帶是一個二維的緊緻流形(即一個有邊界的面),可以嵌入到三維或更高維的流形中。它是一個不可定向的的標準範例,可以看作RP#RP。同時也是數學上描繪纖維...
流形上的斯托克斯公式令 M 為一個可定向分段光滑 n 維流形,令 ω 為 M 上的 n−1 階 C 類緊支撐微分形式。如果 ∂M...
事實上,他還進一步作出了實質的發現:當一個可定向的緊微分流形Mn+2的第1維和第2維法2係數同調群都等於零時,Pn就不能通過微分同胚在Mn+2中實現。...
在中,吳光磊考慮了緊閉可定向黎曼流形上的格拉斯曼(Grassmann)叢的自然黎曼度量具有與叢的局部積結構相配合的局部分解的條件,並在此條件下算出了叢的Betti數。此外...
