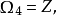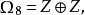定向配邊類(oriented cobordism class)是流形的一種等價類,對於兩個光滑緊定向n維流形M與M′,若存在一個光滑緊的帶邊的定向流形X,使得∂X及其誘導定向在保持定向的同胚之下同胚於M與(-M′)的無交並,則稱M與M′屬於同一個定向配邊類。定向配邊類的這種關係是自反的、對稱的和傳遞的,因此是一個等價關係,在這種等價關係之下的等價類之集記為Ωn,對Ωn中的任意兩個元素{M},{M′},用無交並作為群運算,則Ωn構成一個阿貝爾群,這個群的零元就是空流形的配邊類。例如,可以列出定向配邊類群如下:Ω0≅Z,Ω1=0,Ω2=0,Ω3=0,Ω4≅Z,Ω5=Z/2,Ω6=0,Ω7=0,Ω8≅Z⊕Z,Ω9=(Z/2)⊕(Z/2),Ω10≅Z/2,Ω11≅Z/2。
基本介紹
- 中文名:定向配邊類
- 外文名:oriented cobordism class
- 所屬學科:數學
- 所屬問題:流形上的分析(示性類理論)
- 相關概念:定向流形,配邊理論等
基本介紹,相關理論,托姆基本定理,結構定理,定向配邊不變數,
基本介紹
定向配邊理論的研究對象是所有定向流形的集合,其中所有流形都有兩種定向。如果一種用 表示,另一種則用
表示,另一種則用 表示,它們在這個集合中代表不同的元素。
表示,它們在這個集合中代表不同的元素。


兩個 維閉流形
維閉流形 稱為定向配邊,如果存在一個,
稱為定向配邊,如果存在一個,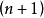 維可定向有邊緣流形X,使得
維可定向有邊緣流形X,使得


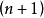



經過托姆、米爾諾(Milnor,John Willard,1931-) 和沃爾的研究, 的結構也完全決定。
的結構也完全決定。

相關理論
托姆基本定理


結構定理





1960年,米爾諾證明 沒有p分量,p為任意奇素數。同年,沃爾證明
沒有p分量,p為任意奇素數。同年,沃爾證明 的2分量中不含4階元素。
的2分量中不含4階元素。


設 為
為 中所有撓元構成的理想,則
中所有撓元構成的理想,則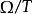 為
為 上多面‘式環,以
上多面‘式環,以 為生成元,其中
為生成元,其中 可取為復
可取為復 維非奇異代數簇。
維非奇異代數簇。






定向配邊不變數
兩個定向閉流形定向配邊若且唯若其所有的施蒂費爾-惠特尼示性數和龐特里亞金示性數對應相等。