流形是局部具有歐幾里得空間性質的空間,在數學中用於描述幾何形體。物理上,經典力學的相空間和構造廣義相對論的時空模型的四維偽黎曼流形都是流形的實例。
基本介紹
發展歷史
定義
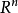


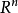



圓周

局部坐標卡

坐標變換

坐標圖集
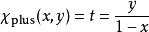




流形反例
重要流形




流形是局部具有歐幾里得空間性質的空間,在數學中用於描述幾何形體。物理上,經典力學的相空間和構造廣義相對論的時空模型的四維偽黎曼流形都是流形的實例。
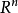








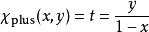







流形是局部具有歐幾里得空間性質的空間,在數學中用於描述幾何形體。物理上,經典力學的相空間和構造廣義相對論的時空模型的四維偽黎曼流形都是流形的實例。...
芬斯勒流形(Finsler manifold)亦稱芬斯勒空間,是一種比黎曼流形更廣泛的度量空間。像黎曼流形一樣,芬斯勒流形的兩點之間的距離定義為連線這兩點的曲線弧長的下確界...
所謂霍普夫流形(Hppf manifold),是指與S2n+1×S1同胚的復流形。...... 霍普夫流形是特殊的復流形。所謂霍普夫流形,是指與S2n+1×S1同胚的復流形。若n=1,...
《流形上的分析》可作為數學專業的研究生和高年級本科生的教材或參考書,也可供物理及某些工科專業的研究生、青年教師和有關工程技術人員參考。...
流形學習,全稱流形學習方法(Manifold Learning),自2000年在著名的科學雜誌《Science》被首次提出以來,已成為信息科學領域的研究熱點。在理論和套用上,流形學習方法都...
微分流形(differentiable manifold),也稱為光滑流形(smooth manifold),是拓撲學和幾何學中一類重要的空間,是帶有微分結構的拓撲流形。 微分流形是微分幾何與微分...
積分流形(integral manifold)是一類子流形。它是由對合分布確定的子流形。流形是一類拓撲空間,它在每一點的附近都與歐氏空間同胚。一般的流形概念,起始於對於可...
組合流形是對於其結構有限制的一類PL流形。PL 流形是具有分片線形結構的流形。...... 組合流形是對於其結構有限制的一類PL流形。PL 流形是具有分片線形結構...
拓撲流形,為最容易定義的流形,它局部看起來象一些“普通”的歐氏空間Rn。形式化的講,一個拓撲流形是一個局部同胚於一個歐氏空間(或上半歐式空間)的拓撲空間。...
同調流形(homology manifold)是一類重要的拓撲空間。拓撲空間是歐幾里得空間的一種推廣。給定任意一個集,在它的每一個點賦予一種確定的鄰域結構便構成一個拓撲空間...
黎曼流形是一黎曼度量的微分流形。設M是n維光滑流形,若在M上給定一個光滑的二階協變張量場g,稱(M,g)為一個n維黎曼流形,g稱為該黎曼流形的基本張量或黎曼...
格拉斯曼流形是代數幾何中的重要研究對象,因數學家格拉斯曼的首次研究而得名。...... 格拉斯曼流形是代數幾何中的重要研究對象,因數學家格拉斯曼的首次研究而得名。...
施坦流形是從多複變函數論角度研究最多的復流形,它是全純凸域在復流形上的推廣。...... 施坦流形是從多複變函數論角度研究最多的復流形,它是全純凸域在...
巴拿赫流形是有限維流形的無窮維推廣,巴拿赫流形一般均指巴拿赫微分流形,光滑流形一般是指C∞流形。...
在數學中,一個凱勒流形(Kähler manifold)是具有滿足一個可積性條件的酉結構(一個U(n)-結構)的流形。特別地,它是一個黎曼流形 、復流形以及辛流形,這三...
線性流形(linear manifold)是幾何學中的常用概念,即Pn中的直線,二維平面,三維平面,…,n-1維平面的統稱。設A是線性空間R中的真子集,若對x,x'∈A,θ,θ'...
本書是微分流形和現代幾何的一本入門教材。本書從微分流形的定義出發,介紹了現代幾何學研究中的各種基本概念和技巧。前兩章為基礎內容,主要介紹流形上的微積分並...
克勒流形是一類重要的復流形,具有克勒度量的復流形稱為克勒流形。例如,Cn中有界域關於伯格曼度量為克勒流形。...
在數學中,特別是在微分幾何和代數幾何中,復流形是具有復結構的微分流形,即它能被一族坐標鄰域所覆蓋,其中每個坐標鄰域能與n維複線性空間中的一個開集同胚,從而...
流形乘積(product of manifolds)是微分拓撲學的一個重要概念。對兩個微分流形的拓撲乘積空間上給出適當的微分構造使之成為微分流形的一般方法。...
《流形拓撲學:理論與概念的實質》是2010年科學出版社出版的圖書,作者是馬天。...... 《流形拓撲學:理論與概念的實質》是一部關於流形的拓撲學專著,較全面和系...
數學上,卡拉比–丘流形(Calabi–Yau manifold)是一個的第一陳類為0的緊緻n維凱勒流形,也叫做卡拉比–丘 n-流形。...
天津流形科技有限責任公司於2017年05月11日成立。法定代表人李夢澤,公司經營範圍包括:計算機網路技術開發、技術轉讓、技術諮詢、技術服務;軟體開發;計算機軟硬體的...
本書作者以微分流形為中心寫了這本書,涉及拓撲學的廣泛的領域並在分析數學、幾何學乃至理論物理學中均可得到重要的套用。本書的主要內容是:微分流形、示性類...
半監督學習中兩種假設之一,另外一種假設是聚類假設。 流形假設是指處於一個很小的局部鄰域內的示例具有相似的性質,因此,其標記也應該相似。這一假設反映了決策...
