基本介紹
- 中文名:菲勒斯流形
- 外文名:Finsler manifold
- 所屬學科:數學
- 所屬領域:微分幾何學
- 別名:芬斯勒空間
基本介紹
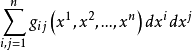

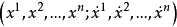
芬斯勒度量

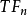


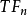
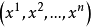

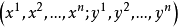
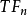

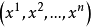

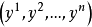

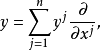
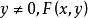
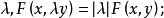
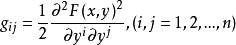


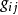

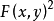
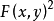
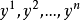
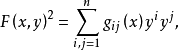

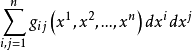

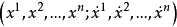

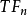


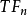
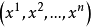

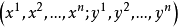
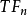

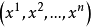

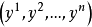

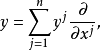
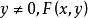
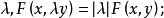
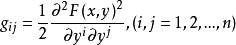


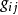

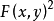
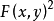
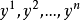
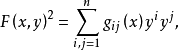
芬斯勒流形(Finsler manifold)亦稱芬斯勒空間,是一種比黎曼流形更廣泛的度量空間。像黎曼流形一樣,芬斯勒流形的兩點之間的距離定義為連線這兩點的曲線弧長的下確界...
芬斯勒度量是黎曼度量的一種推廣。若Fn是n維微分流形,TFn是Fn的切叢,Fn上的芬斯勒度量是定義在切叢TFn上滿足下列條件的連續的實值函式F:設(x1,x2,...,xn)...
僅僅要指出,芬斯勒空間的測地線(即上列積分的極值曲線)的微分方程具有如下的形式: 式中是由F(x,凧)確定的某種函式組。 近年來,無限維的芬斯勒流形在非線性...
芬斯勒主要研究非黎曼幾何學.他建了一種以坐標及其微分的更一般函式來表示的測度,稱為芬斯勒測度一個具有芬斯勒測度的微分流形,稱為芬斯勒空間.他最早以芬斯勒測度來...
芬斯勒結構是巴拿赫向量叢上的範數結構。芬斯勒結構因芬斯勒(Finsler,P. )的工作而得名。設 是巴拿赫流形M上的巴拿赫向量叢, 從ξ上的一個芬斯勒結構是指滿足下述...
希爾伯特-黎曼流形(Hilbert-Riemann manifold)是指定了黎曼度量的希爾伯特流形。...... 黎曼度量是一種特殊的芬斯勒結構。希爾伯特-黎曼流形是特殊的巴拿赫-芬斯勒流形...
全書共十章,前五章介紹了芬斯勒流形、閔可夫斯基空間(即芬斯勒流形的切空間)上的幾何量、陳聯絡,以及共變微分和第二類幾何量、黎曼幾何不變數和弧長的變分等...
芬斯勒空間的曲率(curvature of the Finderspace)一種曲率,它與黎曼流形的曲率類似.在芬斯勒空間式的一點P的向量X沿無窮小迴路平行移動回到P時得到向量X' , X到...
內容包括:微分流形、芬斯勒度量、陳聯絡和結構方程、S曲率、芬斯勒度量的黎曼曲率、芬斯勒度量的射影變換、芬斯勒流形的體積比較定理和基本群、芬斯勒子流形和調和...
設M是巴拿赫流形,‖·‖為TM上的芬斯勒結構,則(M,‖·‖)稱為巴拿赫-芬斯勒流形,或簡稱芬斯勒流形。...
曲面的大量新的調和同態、得到了從拓撲球面或旗流形到旗流形的大量新的調和映射、提出並系列研究了芬斯勒流形上的調和映射理論、建立了芬斯勒流形上三類幾何不變數...
近年來,無限維的芬斯勒流形在非線性分析中有重要作用。一般空間微分幾何學嘉當空間 編輯 在n維空間裡,以(n-1)維超曲面領域的表面積概念為基礎而構成的幾何,稱...
簡介 偽梯度向量場(pseudo-gradient vector field)梯度向量場在不適合用來構造下降流時的一種替代物.當M是一般巴拿赫流形,.f E C2-0 <M, R)時,餘切向量場...
形變引理指在巴拿赫流形上利用泛函的偽梯度向量場對泛函的水平集進行所需形變的一些定理。...
C2-0巴拿赫-芬斯勒流形上任一C1泛函的偽梯度向量場總是存在的。由-V在 上生成的流稱為f的偽梯度下降流,或負偽梯度流,也常簡稱偽梯度流。f在負偽梯度流的...
設M是完備的C2-0芬斯勒流形,f∈C1(M,R)滿足(P.S)條件,𝓕是M的一一個非空子集族。記 若c是有限數,且存在ε0>0,使得𝓕關於收縮映射族 或同胚映射...
當X是完備的芬斯勒流形且f∈C1時,在點yε處有||df(yε)||≤ε。 [1] 艾克蘭德變分原理泛函 編輯 簡單的說, 泛函就是定義域是一個函式集,而值域是實數...
柳斯捷爾尼克一施尼雷爾曼重數定理(Ljustern-ik-Schnirelman multiplicity theorem)利用疇數對流形上泛函的臨界點的個數進行估計的重要定理.設M是完備的巴拿赫一...
柳斯捷爾尼克-施尼雷爾曼重數定理是利用疇數對流形上泛函的臨界點的個數進行估計的重要定理。...
