芬斯勒度量

F_n上的芬斯勒度量是定義在切叢TF_n上滿足下列條件的連續的實值函式F。

基本介紹

• 中文名：芬斯勒度量
• 外文名：Finsler metric
• 適用範圍：數理科學

簡介

芬斯勒度量是黎曼度量的一種推廣。

若F_n是n維微分流形，TF_n是F_n的切叢，F_n上的芬斯勒度量是定義在切叢TF_n上滿足下列條件的連續的實值函式F:設(x¹,x²,...,xⁿ)是F_n上局部坐標系，(x¹,x²,...,xⁿ;y¹,y²,...,yⁿ)是TF_n的點(x,y)的局部坐標，其中(x¹,x²,...,xⁿ)是F_n的點x的局部坐標，(y¹,y²,...,yⁿ)是F_n的點x的切向量y的分量，即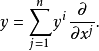

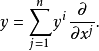
性質

1、在y≠0，F(x,y)可微。

2、對任意實數λ，F(x,λy)=|λ|F(x,y)。

3、以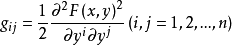為元素的矩陣是正定的。

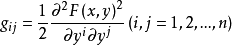
此時，F_n稱為芬斯勒空間，函式F也稱為芬斯勒空間F_n的度量函式。以g_ij為分量的張量稱為F_n的度量張量或基本張量，F(x,y)²稱為基本形式。

當F(x,y)²是y¹,y²,...,yⁿ的二次齊式時，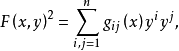

這個芬斯勒度量是黎曼度量。

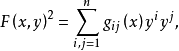
判定

微分流形上存在芬斯勒度量的充分必要條件是它為仿緊的。