巴拿赫-芬斯勒流形

設M是巴拿赫流形，‖·‖為TM上的芬斯勒結構，則(M,‖·‖)稱為巴拿赫-芬斯勒流形，或簡稱芬斯勒流形。

基本介紹

• 中文名：巴拿赫-芬斯勒流形
• 外文名：Banach- Finsler manifold
• 適用範圍：數理科學

簡介

巴拿赫-芬斯勒流形是在切叢上指定了芬斯勒結構的巴拿赫流形。

設M是巴拿赫流形，‖·‖為TM上的芬斯勒結構，則(M,‖·‖)稱為巴拿赫-芬斯勒流形，或簡稱芬斯勒流形。

推廣

切叢上的芬斯勒結構自然誘導出餘切從上的芬斯勒結構。切從上的芬斯勒結構亦稱為芬斯勒度量。它按可誘導出M上的度量：設a:[a,b]→M是C¹曲線（或逐段C¹曲線），則可定義曲線a（從a到b）的長度為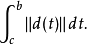

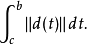
性質

設M連通（否則考慮其每個連通分支），可定義M上任取兩點p和q間的距離為ρ(p,q)=inf{M上從p到q的逐段C¹曲線的長度}，則ρ滿足距離公理，(M,ρ)成為距離空間，且ρ誘導的拓撲與M上原有的拓撲一致。

若距離空間(M,ρ)是完備的，則稱M是完備的巴拿赫-芬斯勒流形。