偽梯度流

偽梯度向量場是梯度向量場在不適合用來構造下降流時的一種替代物，最早由帕萊斯(Palais,R.S.)於1966年給出。

基本介紹

• 中文名：偽梯度流
• 外文名：pseudo-gradient flow
• 適用範圍：數理科學

簡介

偽梯度向量場是梯度向量場在不適合用來構造下降流時的一種替代物。偽梯度向量場的概念及其存在性最早由帕萊斯(Palais,R.S.)於1966年給出。

當M是一般巴拿赫流形，f∈C^2-0(M,R)時，餘切向量場df不能用來構造下降流；

當M是希爾伯特流形而f∈C¹(M,R)時梯度向量場∇f也不能用來構造下降流。偽梯度向量場是克服這兩種困難的工具。

定義

設M是C^2-0巴拿赫-芬斯勒流形，f∈C¹(M,R)，記K為f在M上的所有臨界點所成之集，令= M\K。若V是上的一個C^1-0(切)向量場，且滿足條件：

1.；

2.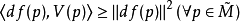，則稱V是f的一個偽梯度向量場。

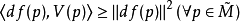
性質

C^2-0巴拿赫-芬斯勒流形上任一C¹泛函的偽梯度向量場總是存在的。

由-V在上生成的流稱為f的偽梯度下降流，或負偽梯度流，也常簡稱偽梯度流。f在負偽梯度流的流線上是下降的。

梯度向量場

梯度向量場是由希爾伯特流形上的C泛函的梯度所形成的切向量場。梯度向量場生成的動力系統比較簡單，它們沒有周期軌，而且所有摩爾斯-斯梅爾梯度向量場（一類簡單的結構穩定的向量場）在所有梯度向量場是開稠的。

設是 n 維歐幾里得空間上的一個光滑函式。由 f 所確定的上的梯度向量場定義為

其中

為 f 的梯度。這裡之所以出現負號是一種習慣用法。