柳斯捷爾尼克一施尼雷爾曼重數定理(Ljustern-ik-Schnirelman multiplicity theorem)利用疇數對流形上泛函的臨界點的個數進行估計的重要定理.設M是完備的巴拿赫一芬斯勒流形,fEC'(M,R)滿足(P. S)條件,對每個n=1,2,""",記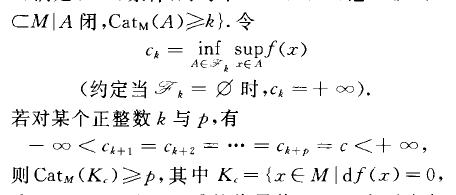
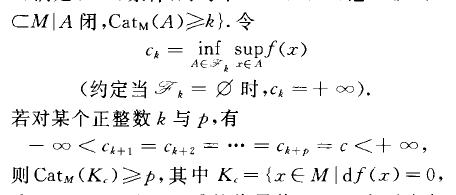
則Cater (K} ) % p,其中K}={xEM}df(x)=0,f(x)=c).此時。是f的臨界值,且K。中至少包含p個不同的臨界點.作為重數定理的特例((p=1時)有:若某個。k是有限數,則。*是f的臨界值. 由重數定理可推出:若f在M上有下界,則f在M上至少有Cater (M)個不同的臨界點.疇數概念與重數定理最早由柳斯捷爾尼克(JIEOCTepHHK, JI.A.)與施尼雷爾曼(IIIuupe}zbMaH, JI. I'.)對緊流形給出,後被帕萊斯(Palais , R. S.)於1966年推廣到巴拿赫流形的情形.
