柳斯捷爾尼克-施尼雷爾曼重數定理

柳斯捷爾尼克-施尼雷爾曼重數定理是利用疇數對流形上泛函的臨界點的個數進行估計的重要定理。

基本介紹

• 中文名：柳斯捷爾尼克-施尼雷爾曼重數定理
• 外文名：Ljusternik- Schnirelman multiplicity theorem
• 適用範圍：數理科學

簡介

柳斯捷爾尼克-施尼雷爾曼重數定理是利用疇數對流形上泛函的臨界點的個數進行估計的重要定理。

設M是完備的巴拿赫-芬斯勒流形，f∈C¹(M,R)滿足(P.S)條件，對每個n=1,2,...，記𝓕_k= {A⊂M|A閉，Cat_M(A)≥k}。令

(約定當F_k= ∅時,c_k=+∞)。若對某個正整數k與p，有-∞<c_k+1=c_k+2=...=c_k+p=c<+∞，則Cat_M(K_e)≥p，其中K_e= {x∈M|df(x)=0,f(x)=c}。此時c是f的臨界值，且K中至少包含p個不同的臨界點。

特例

作為重數定理的特例（p=1時）有：若某個c_k是有限數，則c_k是f的臨界值。

由重數定理可推出：若f在M上有下界，則f在M上至少有Cat_M(M)個不同的臨界點。

疇數概念與重數定理最早由柳斯捷爾尼克與施尼雷爾曼對緊流形給出，後被帕萊斯(Palais,R.S.)於1966年推廣到巴拿赫流形的情形。

流形

流形是局部具有歐幾里得空間性質的空間，在數學中用於描述幾何形體。

在n維Euclid空間中，由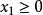定義的半空間用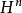表示。Hausdorff空間M，當每點p具有與或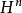同胚的開鄰域U(p)時，稱為n維拓撲流形。U(p)≈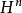（同胚）的點p的全體∂M稱為流形M的邊緣，其補集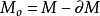稱為M的內部，∂M=Φ的流形稱為無邊緣流形。

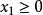
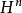
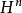
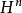
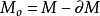
n維流形M的邊緣∂M是n-1維無邊緣流形。緊的無邊緣的連通流形稱為閉流形，非緊的無邊緣的連通流形稱為開流形。存在連通的但非仿緊的拓撲流形。一維的這種流形稱為長直線。