形變引理指在巴拿赫流形上利用泛函的偽梯度向量場對泛函的水平集進行所需形變的一些定理。
基本介紹
- 中文名：形變引理
- 外文名：deformation lemmas
- 適用範圍：數理科學
簡介,內容,偽梯度向量場,
簡介
形變引理是研究臨界點的有力工具，指在巴拿赫流形上利用泛函的偽梯度向量場對泛函的水平集進行所需形變的一些定理。
內容
形變引理方面的結果很多，下述是其中之一。
設M是完備的C2-0芬斯勒流形，f∈C1(M,R)滿足(P.S)條件，設c∈R，Kc={x∈M|df(x)=0,f(x)=c}。U是K的開鄰域，則存在M上的合痕η:[0,1]×M→M與兩個正常數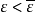
，使得：
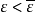
1、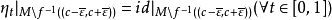
。
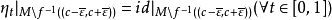
2、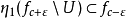
。
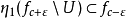
3、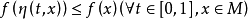
，其中對實數b，fb={x∈M|f(x)≤b}。
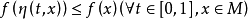
特別地，當Kc=∅時，取U=∅，則上述2成為η1(fc+ε)⊂fc-ε。
偽梯度向量場
(pseudo-gradient vector field)
偽梯度向量場是梯度向量場在不適合用來構造下降流時的一種替代物。
偽梯度向量場的概念及其存在性最早由帕萊斯(Palais,R.S.)於1966年給出。
當M是一般巴拿赫流形，f∈C2-0(M,R)時，餘切向量場df不能用來構造下降流；
當M是希爾伯特流形而f∈C1(M,R)時梯度向量場∇f也不能用來構造下降流。偽梯度向量場是克服這兩種困難的工具。
