芬斯勒結構

芬斯勒結構是巴拿赫向量叢上的範數結構，因芬斯勒(Finsler,P.)的工作而得名。

基本介紹

• 中文名：芬斯勒結構
• 外文名：Finsler structure
• 適用範圍：數理科學

簡介

芬斯勒結構是巴拿赫向量叢上的範數結構。芬斯勒結構因芬斯勒(Finsler,P. )的工作而得名。

設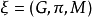 是巴拿赫流形M上的巴拿赫向量叢， 從ξ上的一個芬斯勒結構是指滿足下述條件的連續函式：

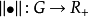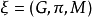
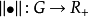
1、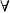p∈M，‖·‖_p=‖·‖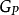是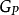上的一個等價範數；

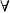
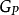
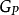
2、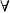p₀∈M，對於p₀在M上的任意使得G在其上可平凡化的鄰域U與任意的k>1，有p₀的鄰城V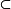U，使得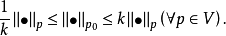

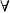
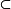
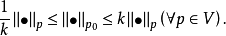
性質

當巴拿赫流形M仿緊時，叢ξ上芬斯勒結構總是存在的。

巴拿赫向量叢

巴拿赫向量叢是每點處的纖維均拓撲線性同構於某巴拿赫空間且局部平凡的叢。

一個叢指的是三元組ξ=(G,π,B)，其中G和B是拓撲空間，π:G→B是連續滿映射。G和B分別稱為叢ξ的全空間與底空間，π稱為投影。對每點b∈B，π^-1(b)稱為叢ξ在點b的纖維，記為G_b。設ξ=(G,π,B)是一個叢，稱叢ξ=(G,π,B)為巴拿赫向量叢。