基本介紹
- 中文名:凱勒流形
- 外文名:Kähler manifold
- 分類:微分幾何、黎曼幾何
- 領域:數理科學
概念

定義
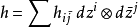
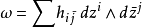
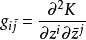
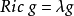
例子
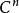
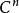
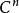

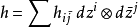
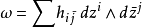
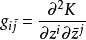
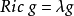
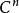
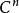
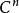
在數學中,一個凱勒流形(Kähler manifold)是具有滿足一個可積性條件的酉結構(一個U(n)-結構)的流形。特別地,它是一個黎曼流形 、複流形以及辛流形,這三...
數學中,里奇平坦流形(Ricci-flat manifold)是里奇張量為零的黎曼流形。在物理學中,它們代表了愛因斯坦方程在任何維數之黎曼流形且宇宙常數為零的類比,其所具有的...
數學上,卡拉比–丘流形(Calabi–Yau manifold)是一個的第一陳類為0的緊緻n維凱勒流形,也叫做卡拉比–丘 n-流形。...
凱勒結構,也稱凱勒流形。在數學中,一個凱勒流形(Kähler manifold)是具有滿足一個可積性條件的酉結構(一個U(n)-結構)的流形。特別地,它是一個黎曼流形、...
1976年解決關於凱勒-愛因斯坦度量存在性的卡拉比猜想,其結果被套用在超弦理論中,對統一場論有重要影響。第一陳類為零的緊緻凱勒流形稱為卡拉比-丘流形,在數學與...
數學上,霍奇理論是光滑流形M的代數拓撲的研究的一個方面。...... 凱勒流形:在數學中,一個凱勒流形(Kähler manifold)是具有滿足一個可積性條件的酉結構(一個...
辛幾何(symplectic geometry)與代數幾何和微分幾何是平行的三個數學分支,是研究辛流形(symplectic manifold)的幾何與拓撲性質的學科。它的起源和物理學中的經典力學...
5.單值化問題,以及非負解析雙截曲率的凱勒流形的幾何的研究。6.三維流形上Ricci flow with surgery 的研究。這些學術論文發表在國際權威的數學雜誌 Journal of ...
引進了完備凱勒流形的代數幾何化,並與鐘家慶合作證明了有限體積完備凱勒流形的緊緻化定理。在代數幾何方面透過極小有理曲線簇的幾何理論證明了不可約緊埃爾米特對稱...
克勒-愛因斯坦度量一類特殊的克勒度量,設(M,g)是克勒流形,S為里奇曲率張量,若S滿足S=ρg,則稱g為M上的克勒-愛因斯坦度量,這時,(M,g)稱為克勒-愛因斯坦流形...
在日本學者村上信吾工作的基礎上,許以超給出了在約化李群可遞作用下的凱勒流形的完全分類。他還在二維復歐幾里得空間中加上圖倫(Thullen)條件的有界域上考慮了...
在微分幾何中,對一個給定的結構群 G,n 維流形 M 上一個 G-結構是 M 的切標架叢 FM(或 GL(M))的一個 G-子叢。G-結構的概念包括了許多流形上其它...
調和映射(harmonic map)黎曼流形之間的一類十分重要的可微映射。數學上,在黎曼流形M和N之間的一個(光滑)映射,稱為調和映射。...
定理和小平嵌入定理,對緊復曲面做出了系統的分類,並發展了高維複流形的形變...完成一系列重要工作,其中包括證明曲面的黎曼-羅赫定理、證明狹義凱勒流形是代數...
體積元(volume element)是一種外微分形式,微分流形上與定向相符的外微分形式。更一般地,一個體積元是流形上一個測度。...
在一個殆凱勒流形上,可以將這個分解寫成 h = g + iω,這裡 h 是埃爾米特形式,g 是黎曼度量,i 是殆復結構,而ω 是殆辛結構。...
傅吉祥在復幾何,特別在非凱勒復幾何的研究領域做出了一系列國際領先的具有原創性的研究成果。如他與丘成桐教授合作,首次在非Kahler流形上解出了Strominger方程組,解決...
形式空間的例子有球面、H-空間、對稱空間、緊凱勒流形等(Deligne 等人 1989)。楔積和直積都保有形式性;對於流行而言,連通和也保有形式性。...
射影空間微分結構(differential structure ofprojective space)是微分流形的重要例子。它在拓撲學各分支及其相關學科中是常見的。...
主要科研成果包括:構造出第一個李代數上非對稱雙極化的例子,解決了日本數學家金行壯二提出的待解問題;系統研究了齊性仿凱勒流形的幾何性質,最終得到了半單情形的...
