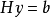埃爾米特形式(Hermite Normal form)複流形上的一種特殊雙線性形式。
基本介紹
- 中文名:埃爾米特形式
- 外文名:Hermite Normal form
- 定義:特殊雙線性形式
- 學科:數理科學
- 分類:行埃爾米特形式、列埃爾米特形式
- 領域:線性代數
簡介,定義,行埃爾米特形式,列埃爾米特形式,Hermite範式的存在性和唯一性,示例,算法,應用程式,格子計算,整數解線性系統,
簡介
線上性代數中,埃爾米特形式是整數Z上矩陣的簡化階梯形式的一個類似形式。就像簡化的階梯形式可以用來解決關於線性系統的解的問題Ax = b其中x在Rn中, 埃爾米特形式可以解決關於線性系統Ax = b的解的問題,其中這個時間x僅限於具有整數坐標。 埃爾米特形式的其他套用包括整數規劃、密碼學,和抽象代數。
定義
行埃爾米特形式
如果存在平方單模矩陣U,其中H = UA且H具有以下限制,則具有整數項的m×n矩陣A具有(行)埃爾米特形式(HNF)H:
- H是上三角(即,對於i> j,hij= 0),並且任何零行都位於任何其他行的下面。
- 非零行的前導係數(從左邊開始的第一個非零輸入,也稱為樞軸)始終嚴格地位於其上一行的前導係數的右側。
- 樞軸下方的元素為零,樞軸上方的元素非負,嚴格小於樞軸。
列埃爾米特形式
如果有一個正方形的單模矩陣U,其中H = AU和H有以下限制,那么具有整數項的m×n矩陣A具有(列)Hermite範式(HNF)H:
- H是下三角形,對於i <j,hij= 0,任意的零列都位於右邊。
- 非零列的前導係數(從頂部開始的第一個非零的入口,也稱為支點)始終嚴格低於之前列的前導係數。
- 樞軸右側的元素為零,樞軸左側的元素非負,嚴格小於樞軸。
請注意,行樣式定義具有在左邊乘以A的單模矩陣U(意味著U在A的行上作用),而列樣式定義在A的列上具有單模矩陣行為。Hermite範式的兩個定義只是彼此的轉置。
Hermite範式的存在性和唯一性
每個具有整數項的m×n矩陣A具有唯一的m×n矩陣H(HNF),使得對於某個平方單模矩陣U,H = UA。
示例
在下面的例子中,H是矩陣的埃爾米特正常形式A,和U是單模矩陣,使得UA = H。
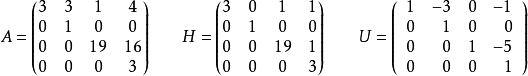
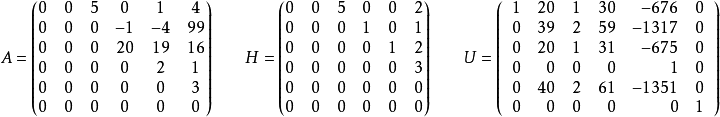

如果A只有一行,則H = A或H = -A,取決於A的單行是否具有正的或負的超前係數。
算法
有許多算法計算可追溯到1851年的Hermite標準形式。直到1979年,才開始計算在強多項式時間運行的Hermite標準形式的算法;也就是說,計算Hermite範數的步數由輸入矩陣的維數中的多項式來界定,算法所使用的空間(中間數)由二進制編碼中的多項式輸入矩陣中數字的大小。一類算法是基於高斯消元的,因為特殊的基本矩陣被重複使用。所述的LLL算法也可以用來有效地計算Hermite範式。
應用程式
格子計算
典型的晶格中 具有形式
具有形式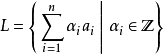 其中
其中 是
是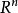 。如果矩陣A的列是
。如果矩陣A的列是 ,則格可以與矩陣的列相關聯,並且A被認為是L的基礎。由於Hermite範式是唯一的,所以可以用來回答關於兩個格點描述的許多問題。接下來,
,則格可以與矩陣的列相關聯,並且A被認為是L的基礎。由於Hermite範式是唯一的,所以可以用來回答關於兩個格點描述的許多問題。接下來, 表示由A的列生成的格。因為基礎在矩陣A的列中,所以必須使用列式Hermite範式。給定一個格點A和A'的兩個基礎,等價問題是決定是否
表示由A的列生成的格。因為基礎在矩陣A的列中,所以必須使用列式Hermite範式。給定一個格點A和A'的兩個基礎,等價問題是決定是否 這可以通過檢查A和A'的列式Hermite標準形式是否相同直到添加零列來完成。這個策略對於決定格是否是一個子集也是有用的
這可以通過檢查A和A'的列式Hermite標準形式是否相同直到添加零列來完成。這個策略對於決定格是否是一個子集也是有用的 若且唯若
若且唯若  ),判斷一個向量v是否在一個格中(
),判斷一個向量v是否在一個格中( 若且唯若
若且唯若  )和其他計算。
)和其他計算。

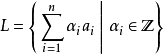

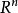







整數解線性系統
線性系統Ax = b的具有整數解X若且唯若所述系統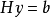 具有整數溶液y其中Uy的= X和H是列式的隱士正常形式H。檢查Hy = b是否具有整數解比Ax = b容易,因為矩陣H是三角形的。
具有整數溶液y其中Uy的= X和H是列式的隱士正常形式H。檢查Hy = b是否具有整數解比Ax = b容易,因為矩陣H是三角形的。