射影空間微分結構

射影空間微分結構(differential structure ofprojective space)是微分流形的重要例子。它在拓撲學各分支及其相關學科中是常見的。

基本介紹

• 中文名：射影空間微分結構
• 外文名：differential structure ofprojective space
• 領域：數學
• 學科：拓撲學
• 性質：微分流行

概念

射影空間微分結構(differential structure ofprojective space)是微分流形的重要例子。它在拓撲學各分支及其相關學科中是常見的。若在Rⁿ⁺¹-{0}中規定等價關係“～：對於x，y∈Rⁿ⁺¹-{0}，x～y若且唯若存在λ∈R，x=λy，則商拓撲空間R-{0}/～稱為n維(實)射影空間，記為RPⁿ。若π： Rⁿ⁺¹-{0}→RPⁿ為自然投影，即對於x∈Rⁿ⁺¹-{0}，π(x)=[x]是x所屬的等價類，則按下述方式RP是n維微分流形，對於i=1，2，…，n+1，記：

與φ_i： U_i→R，對於[x]∈U_i，x=(x₁，x₂，…，x_n+1)，

從而Φ={(U_i，φ_i)|i=1，2，…，n+1}是RPⁿ的一個(光滑)圖冊，由此決定RPⁿ上的(光滑)微分構造，從而使得RPⁿ是n維微分流形。特別地，RP²為2維射影平面。類似地，可定義復射影空間CPⁿ，它是2n維(實)微分流形。

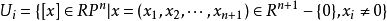
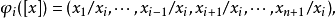
射影空間

射影空間是整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形)，為方便起見引入無窮遠點的概念，即規定平面上每條直線上有一個無窮遠點，兩條直線平行就是相交於無窮遠點，所有無窮遠點組成一條無窮遠直線。這種構造方法還可以推廣到高維空間，建立n維(實)射影空間P_R.在n維射影空間中常採用齊次坐標(X₀∶X₁∶…∶X_n)，其中X₀，X₁，…，X_n不全為0；若a≠0，則(aX₀∶aX₁∶…∶aX_n)與(X₀∶X₁∶…∶X_n)表示同一個點。因此n維(實)射影空間同構於(R-{0})/R.進一步的研究表明P_R是緊緻解析流形。若令U_i(0≤i≤n)為P_R中坐標X_i≠0的點全體，則U_iR，且U₀，U₁，…，U_n組成P_R的一個開覆蓋。上述構造方法可以推廣到任意體K上，建立K上的n維射影空間P_K。在概形理論中，還將射影空間建立在整數環Z上，即建立射影概形Pn_Z。由此對任意概形X可以建立Pⁿ_X，它是X和Pⁿ_Z(在Spec Z上)的纖維積.特別地，若X=Spec K(K為域)，則Pⁿ_X=Pⁿ_K。

由於射影空間的性質非常豐富難以全面列舉，僅舉數例如下：

1.P_R同胚於圓，P_C可看做添上無窮遠點的複平面，同胚於球面。

2.P_R是單側曲面，可以同胚地嵌入四維空間R⁴，但不能同胚地嵌入三維空間R³，P²_C是代數極小曲面.

3.P_C是凱勒流形，它的閉解析子空間都是代數的。

4.對任意域k，P_k是齊性空間，其切叢由整體向量場生成，其自同構群為射影群PSL(n+1，k)，其皮卡群Pic(Pⁿ_k)Z。

微分流形

設M是仿緊豪斯道夫 (Hau-sdorff)空間，且是拓撲流形，稱A= {(U_α，Ф_α)|α∈P}是它的地圖，如果{U_α|α∈P}是M的開覆蓋，Ф_α是從U_α到n維歐氏空間R的某開集上的同胚。(U_α，Φ_α)稱為坐標卡。如果兩個坐標卡 (U_α，Ф_α)，(Uβ，Φ_β) 滿足U_α∩U_β≠Φ，則稱Φ_β·Ф_α：Φ_α(U_α∩U_β) →Φ_β(U_α∩U_β) 和Φ_α·Φ_β： Φβ(U_α∩U_β) →Ф_α(U_α∩U_β) 為U_α∩U_β上的坐標變換。如果A的所有坐標變換都是C可微的，則稱A為一個C地圖，其中1≤r≤∞。r也可等於ω，此時A稱為解析地圖。拓撲流形M的坐標卡 (U，Φ) 稱為與A是Cr相容的，如果任意(U_α，Φ_α) ∈A，坐標變換Φ·Φ_αΦ_α·Φ均C可微。拓撲流形M的C地圖A稱為最大的，如果它包含M的所有與之C相容的坐標卡。M上的最大C地圖A稱為M的C微分結構。(M，A)稱為C微分流形，或簡稱為C流形。當r=∞時，C微分結構也稱為光滑結構，C流形也稱為光滑流形。r=ω時，C結構也稱為解析結構，C流形稱為解析流形。C流形(M，A)有時也簡記為M。

從直觀上看，拓撲流形是局部歐氏空間，局部之間用同胚映射(坐標變換)貼上在一起。n維C流形，不僅局部同胚於n維歐氏空間，而且局部之間是用C光滑、且其逆也C光滑的坐標變換貼上在一起。

兩個C流形M和N，f：M→N是連續映射，且任一點P∈M，有包含P點的M中的坐標卡(U，Φ)以及包含f(P)的N中的坐標卡(V，∅)，使得f(U)⊂V，同時，映射∅°f°Φ_-1：Φ(U)→∅(V)是C光滑的(1≤r≤∞或r=ω)，則稱f是C映射。C映射也稱為光滑映射，C映射也稱為解析映射。

拓撲學

研究幾何圖形在一對一的雙方連續變換下保持不變性質的一門數學分支。這種性質被稱為拓撲性質。最初屬於幾何學，叫做“位置分析”或“形勢分析”，1847年德國數學家利斯廷改稱為“拓撲學”，暗指和地形、地勢相類似的學科。現在已發展成為研究連續性現象的數學分支，常指與拓撲有關的研究領域。19世紀末已出現點集拓撲學與組合拓撲學兩個方向，前者把幾何圖形看作是點的集合，又常把這個集合看作是一個空間，後來演化成為一般拓撲學。後者把幾何圖形看作是由較小的部分組成的，研究這些部分的性質，後來發展成為代數拓撲學。在歷史上組合拓撲學的研究要先於點集拓撲學。

1679年萊布尼茨發表《幾何特性》一文，試圖闡述幾何圖形的基本幾何性質，採用特別的符號來表示它們，並對它們進行運算來產生新的性質。他把他的研究叫做位置分析或位置幾何學，並另外宣稱應建立一門能直接表示位置的真正幾何的學問，這是組合拓撲學的先聲。

1736年歐拉解決了著名的柯尼斯堡七橋問題。這原來是一個智力遊戲題，問能否在散步中連續地經過柯尼斯堡城內一條河上的七座橋且每座橋只走一次。歐拉解決問題的方式卻具有拓撲意義。他簡化了這一問題的表示法，用點代表陸地，用線段或弧代表橋，將問題改變成：能否一筆畫出這個圖。歐拉證明了這一圖形是不能一筆畫出的，並作了推廣，給出任何一組給定的點和線(弧)能否一筆畫出的判別法則，成為組合拓撲學的先聲。1750年歐拉又得到了以他的名字命名的凸多面體定理：面數+頂角數-棱數=2，第二年給出一種簡單的歸納證明，1752年發表出來。後人發現笛卡兒約在1635年就已在手稿中表述過這一公式，但他的結果直到1860年才被整理髮表出來。歐拉多面體定理表述了幾何圖形的一個基本組合性質，其目的是利用這一關係將多面體進行分類，這類問題成為19世紀後半葉拓撲學研究的主要問題。長期以來，講述歐拉多面體定理的證明一般採用柯西於1811年給出方法，即去掉一個面的內部，將剩下的圖形鋪在一個平面上，把圖形分割為三角形，然後在一個個地抹掉三角形時計算這個數的改變，得到所需的結論。該證明假設了任一閉的凸多面體同胚於球面，有不足之處。只因其簡單直觀而被廣泛引用。另一個較簡單的證明利用的是球心投影法，據說是法國數學家勒讓德最先給出的。1833年高斯在電動力學中用線積分定義了空間中兩條封閉曲線的環繞數，為拓撲學研究又提供了一個實例。