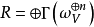Pn(C)的一個子集,若它可以表示為定義在Cn+1中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pn(C)的代數子集。
基本介紹
- 中文名:射影代數簇
- 外文名:projective algebraic variety
基本介紹,代數簇相關介紹,
基本介紹
代數簇(algebraic variety)是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離、有限型k概形,這裡的基域k往往被取作代數閉域。若一個代數簇又是射影、擬射影、仿射或正常k概形,則把這個代數簇相應地稱為射影、擬射影、仿射、完備(代數)簇。射影簇必定是完備簇,反之則不然。永田定理斷言:對任意的代數簇X,必存在一個完備簇,使得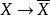 是開浸入。代數簇的概念最早是在20世紀20年代由范·德·瓦爾登(Van der Waerden,B.L.)和諾特(Noether,E.)等提出的,以後又經過韋伊(Weil,A.)、塞爾(Serre,J.P.)等人的發展,直至格羅騰迪克(Grothendieck,A.)把它納入概形體系,才得到上述的現代定義。
是開浸入。代數簇的概念最早是在20世紀20年代由范·德·瓦爾登(Van der Waerden,B.L.)和諾特(Noether,E.)等提出的,以後又經過韋伊(Weil,A.)、塞爾(Serre,J.P.)等人的發展,直至格羅騰迪克(Grothendieck,A.)把它納入概形體系,才得到上述的現代定義。
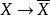
定義  中不可約代數集合(加上它的誘導拓撲)叫做射影代數簇(或簡稱射影簇)。 射影簇的開子集叫做擬射影簇,射影簇或擬射影簇的維數指的是它作為拓撲空間的維數。
中不可約代數集合(加上它的誘導拓撲)叫做射影代數簇(或簡稱射影簇)。 射影簇的開子集叫做擬射影簇,射影簇或擬射影簇的維數指的是它作為拓撲空間的維數。

推論設Y是(擬)射影簇,則Y具有開覆蓋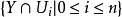 ,其中每個
,其中每個 由上述映射
由上述映射 均同胚於(擬)仿射簇。
均同胚於(擬)仿射簇。
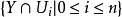


代數簇相關介紹
設P是複數域C上的一個n維射影空間。我們可以給P確定一組齊次坐標 ,關於
,關於 的一個多項式
的一個多項式 稱為d次齊次多項式,如果F的每一項的總次數都是d。在這種情況下,使F為零的那些
稱為d次齊次多項式,如果F的每一項的總次數都是d。在這種情況下,使F為零的那些 就構成P中的一個幾何流形,P中對應於這樣的
就構成P中的一個幾何流形,P中對應於這樣的 的一個點也叫做F的一個零點。
的一個點也叫做F的一個零點。





一般地,我們可以考慮P中由一組(有限或無限多個,不一定同次)齊次多項式的公共零點所定義的流形。這樣的一個流形叫做P中的(射影)代數集,因為兩個代數集的並也是一個代數集,在很多情形下人們只需要考慮不可約的代數集,也就是不能表示成兩個真子代數集之並的代數集,這樣的代數集就叫做P中的射影代數簇,它是代數幾何研究的基本對象。
設V是一個代數簇。代數幾何感興趣的不僅是V作為拓撲流形的幾何特性,而且更多的是V上的代數結構,這個代數結構是由V上的所有有理函式(或稱代數函式)所確定的。每個有理函式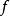 都可以表示成兩個相同次數的齊次多項式的商,並且我們要求分母不在V上恆等於零,於是
都可以表示成兩個相同次數的齊次多項式的商,並且我們要求分母不在V上恆等於零,於是 在V的一個處處稠密的開子集上有定義。這是一種代數幾何特有的開子集,即所謂扎里斯基開子集。
在V的一個處處稠密的開子集上有定義。這是一種代數幾何特有的開子集,即所謂扎里斯基開子集。
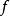

V上的所有有理函式自然地構成一個域 ,稱為V的有理函式域。我們可以定義V的維數為
,稱為V的有理函式域。我們可以定義V的維數為 在複數域C上的超越次數,事實上這樣定義的維數就等於V作為複數域上解析流形時的復維數。1維的代數簇又稱為代數曲線,2維的稱為代數曲面,3維的稱為曲體。
在複數域C上的超越次數,事實上這樣定義的維數就等於V作為複數域上解析流形時的復維數。1維的代數簇又稱為代數曲線,2維的稱為代數曲面,3維的稱為曲體。


另一方面,代數幾何關心的首先是代數簇V上的代數結構而不是V在空間P中的嵌入。在這個意義下,如果我們有兩個代數簇V和W之間一個一一映射 ,它把W上的有理函式對應成V上的有理函式且反之亦然,則
,它把W上的有理函式對應成V上的有理函式且反之亦然,則 被看成是V和W之間的一個同構映射並且V和W因為同構而被認為是代表了同一個代數簇。例如,射影直線
被看成是V和W之間的一個同構映射並且V和W因為同構而被認為是代表了同一個代數簇。例如,射影直線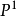 和
和 中由方程
中由方程


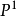


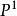
更一般地,我們有兩個代數簇V,W之間的態射概念:一個映射 稱為態射(morphism),如果它誘導W和V的代數結構之間的一個同態,也就是說對於W上的每個有理函式
稱為態射(morphism),如果它誘導W和V的代數結構之間的一個同態,也就是說對於W上的每個有理函式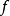 ,複合映射
,複合映射 是V上的有理函式。態射是代數幾何中最基本的映射概念,但很多時候它的條件顯得太強,所以我們有更一般的有理映射概念:對於有理映射
是V上的有理函式。態射是代數幾何中最基本的映射概念,但很多時候它的條件顯得太強,所以我們有更一般的有理映射概念:對於有理映射 ,我們只要求
,我們只要求 是V的一個扎里斯基開子集到W的映射,但當然仍要求
是V的一個扎里斯基開子集到W的映射,但當然仍要求 是V上的有理函式。特別地,如果有理映射
是V上的有理函式。特別地,如果有理映射 有一個有理逆映射,我們稱V和W是雙有理等價的。這時雖然V和W不一定同構,但它們的區別其實很小,比如說有理函式域
有一個有理逆映射,我們稱V和W是雙有理等價的。這時雖然V和W不一定同構,但它們的區別其實很小,比如說有理函式域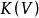 和
和 就是同構的。
就是同構的。

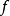





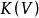

雙有理等價概念對於代數簇的分類問題有著關鍵的意義:一般來說,任一代數簇都有無限多個與其雙有理等價但不同構的代數簇,但因為雙有理等價的代數簇在整體上有相當重要的共同性質而它們的不同只是局部的,可以很自然地把這樣的代數簇看成是同一類的,所以通常所說的代數簇的分類實際上是對代數簇的雙有理等價類的分類。此外,根據著名的廣中平佑奇點解消定理,任意代數簇都雙有理等價於一個光滑代數簇(或稱非奇異代數簇),即沒有奇點的代數簇。這樣至少在理論上,對代數簇的雙有理等價類的分類及其整體性質的研究就可以化為對光滑代數簇的雙有理等價類的這樣的研究,從而避免了局部的奇異點的存在對整體性質研究可能帶來的干擾。在曲線和曲面的情形,這樣的考慮確實是很有效的,雖然我們下面可以看到,從三維情形開始,僅考慮光滑簇是不夠的,必須同時允許一些特殊的奇異點的存在才能克服由於沒有合理的極小模型而帶來的困難。
如果說代數簇V上有理函式定義了V的基本代數結構的話,對研究V的整體性質並對其進行分類的最重要的工具是V上的層(sheaf)。其中人們研究得最多的是局部自由層,就是由V上的某個解析向量叢的所有局部截面(local section)所構成的層,這裡V上的一個解析向量叢是一個解析空間M(可以理解為帶奇點的解析流形),以及從M到V的一個解析映射 ,使得對於V的每個點P,
,使得對於V的每個點P,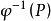 是一個具有固定維數r的復向量空間。數r就叫做M的(或者對應的局部自由層的)秩。事實上,取局部截面的過程構成了V上的所有解析向量叢和所有局部自由層所成的集合之間的一個一一對應,所以有時人們往往不加區別地混用向量叢和局部自由層的概念。當V為光滑代數簇時,向量叢的一個明顯的例子是V上的切空間構成的秩為
是一個具有固定維數r的復向量空間。數r就叫做M的(或者對應的局部自由層的)秩。事實上,取局部截面的過程構成了V上的所有解析向量叢和所有局部自由層所成的集合之間的一個一一對應,所以有時人們往往不加區別地混用向量叢和局部自由層的概念。當V為光滑代數簇時,向量叢的一個明顯的例子是V上的切空間構成的秩為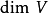 的切叢,對應於V的切層
的切叢,對應於V的切層 。這時V上的所有一階微分形式也自然構成一個秩為
。這時V上的所有一階微分形式也自然構成一個秩為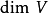 的局部自由層
的局部自由層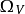 。
。

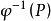
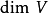

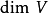
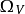
當局部自由層L的秩為1時,L稱為可逆層,相應的向量叢稱為線叢。V上所有可逆層的全體以張量積為運算自然地形成一個群,這就是V的皮卡群 ,其單位元對應的是V上所有有理函式構成的可逆層,稱為平凡層。
,其單位元對應的是V上所有有理函式構成的可逆層,稱為平凡層。

可逆層是最常見也是最有用的層,因為它們與代數簇到射影空間中的映射有著密切的關係:
設L為代數簇V上的一個可逆層.L中的所有整體截面(在V上處處有定義的截面)構成複數域上的一個有限維的向量空間,記為 或
或 ,它的維數記為
,它的維數記為 ,當
,當 非空時,這些整體截面自然地定義了V到射影空間中的一個有理映射
非空時,這些整體截面自然地定義了V到射影空間中的一個有理映射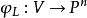 ,這裡
,這裡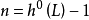 。特別當
。特別當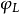 為嵌入映射時,L稱為非常豐富層(very ample)。反之,若
為嵌入映射時,L稱為非常豐富層(very ample)。反之,若 是一個嵌入態射,則
是一個嵌入態射,則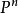 中的一次齊次形式自然地誘導V上的一個非常豐富層L,使得
中的一次齊次形式自然地誘導V上的一個非常豐富層L,使得 ,所以V上的非常豐富層一一對應於V在射影空間中的表示。
,所以V上的非常豐富層一一對應於V在射影空間中的表示。




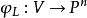
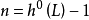
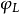

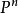

假設V是一個維數為d的光滑代數簇,則V上所有的局部d階外微分形式構成一個可逆層 ,叫做V的典範層,它所誘導的有理映射稱為典範映射。我們有
,叫做V的典範層,它所誘導的有理映射稱為典範映射。我們有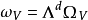 。一般地,對於任一正整數n,我們有n-典範層
。一般地,對於任一正整數n,我們有n-典範層 及其對應的n-典範映射。
及其對應的n-典範映射。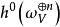 記為
記為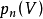 ,或
,或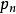 。而當n=1時,
。而當n=1時,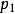 又可記為
又可記為 ,稱為V的幾何虧格。所有這些n-典範層以及n-典範映射在V的同構意義下都是唯一確定的,因此是V上重要的幾何對象。不僅如此,所有的
,稱為V的幾何虧格。所有這些n-典範層以及n-典範映射在V的同構意義下都是唯一確定的,因此是V上重要的幾何對象。不僅如此,所有的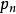 都是雙有理不變數,它們對於雙有理等價的代數簇是不變的。於是下面的典範模型也是雙有理不變的:
都是雙有理不變數,它們對於雙有理等價的代數簇是不變的。於是下面的典範模型也是雙有理不變的:

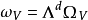

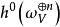
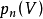
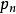
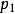

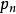
設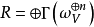 ,這裡求和是對所有大於或等於1的n作的。我們假設R不是空集,則R是C上的一個無限維向量空間,而且n-典範層之間的張量積關係在R上誘導了一個分次環結構,稱為V的典範環。在低維的情形,人們已證明R是有限生成的,這時R可以自然地定義一個射影代數簇
,這裡求和是對所有大於或等於1的n作的。我們假設R不是空集,則R是C上的一個無限維向量空間,而且n-典範層之間的張量積關係在R上誘導了一個分次環結構,稱為V的典範環。在低維的情形,人們已證明R是有限生成的,這時R可以自然地定義一個射影代數簇 ,這就是V的典範模型,它的維數不超過
,這就是V的典範模型,它的維數不超過 。
。