G-結構

在微分幾何中，對一個給定的結構群 G，n 維流形 M 上一個 G-結構是 M 的切標架叢 FM（或 GL(M)）的一個 G-子叢。

G-結構的概念包括了許多流形上其它結構，其中一些是用張量場定義的。例如，對正交群，一個 O(n)-結構定義了一個黎曼度量；而對特殊線性群，一個 SL(n,R)-結構就是一個體積形式；對平凡群，一個 {e}-結構由流形的一個絕對平行化組成。

一些流形上的結構，比如復結構，辛結構，或 凱勒結構，都是 G-結構帶上附加的可積性條件。

物理學中的術語是規範群。

基本介紹

• 中文名：G-結構
• 外文名：G-structure on a manifold
• 適用領域：微分幾何
• 相關概念：主叢理論

主叢和G-結構

儘管主叢理論在G-結構的研究中的角色很重要，但兩個概念是不同的。一個G-結構是一個切標架叢的主子叢，但是G-結構叢“由切標架組成”的事實被視為數據的一部分。例如，考慮Rⁿ上兩個黎曼度量。伴隨的 SO(n)-結構是同構若且唯若度量是同構的。但是，因為Rⁿ是可縮的，故下面的 SO(n)-叢作為主叢總是同構。

兩個理論的這個基本差別能夠被在G-結構下面的G-叢上添加一個額外的數據：焊接形式（solder form）記錄。焊接形式是用一個從M的切叢到配向量叢的典範同構將G-結構下面的G叢繫於流形自身的局部幾何上。儘管焊接形式不是一個聯絡形式，經常可以視為一個聯絡形式的前身。

詳細說來，假設Q是G-結構的主叢。如果Q是實現為M的切叢的壓縮，那么焊接形式是標架叢的重言形式由包含映射的拉回給出。抽象地，如果將Q視為與它作為一個標架叢實現獨立的一個主叢，那么焊接形式由G在Rⁿ上的一個表示 ρ 以及一個叢同構 θ:TM→Q×_ρRⁿ組成。

可積性條件

流形上不少結構，比如復結構，辛結構，或凱勒結構，均是G-結構附加一個可積性條件。沒有相應的可積性條件，這些結構稱為一個“殆（幾乎）”結構，比如殆復結構，殆辛結構，或殆凱勒流形。

特別地，一個辛流形結構是比一個辛群的G-結構更強的概念。流形上一個辛結構是M上一個非退化2形式ω（這是一個{\displaystyle Sp}-結構，或殆辛結構），以及額外條件 dω= 0；後者稱為可積性條件。

類似地，葉狀結構對應於G-結構為分塊矩陣以及可積性條件，這樣便可利用弗羅貝尼烏斯定理。

G-結構的同構

M的保持G-結構的微分同胚集合稱為這個結構的“自同構群”。對一個O(n)-結構它們就是黎曼度量的等距群，而一個 SL(n,R)-結構為保持體積的映射。

設P是流形M上一個G-結構，Q是流形N上一個G-結構。那么G-結構的同構是一個微分同胚f:M→N，使得線性標架的前推f_*:FM→FN的限制給出了P到Q的一個映射（注意只要Q在f_*的像中）。G-結構P與Q是局部同構如果M有一個開集覆蓋U和一族微分同胚f_U:U→f(U) ⊂N使得f_U誘導了一個同構P|_U→Q|_f(U)。

一個G-結構的自同構是G-結構P和自己的同構。自同構經常在研究幾何結構的變換群中出現，因為流形上許多重要的幾何結構可實現為G-結構。

如果G-結構P有一個由可交換向量場(V₁,...,V_n) 組成的整體截面，則稱其為平坦G-結構。若一個G-結構局部同構於平坦G-結構，則稱為可積的（或“局部平坦”）。

一類廣泛的等價問題可以用G-結構語言闡述。例如，一對黎曼流形是（局部）等價等且僅當 它們的正交標架叢是（局部）同構的G-結構。在這種看法下，解決一個等價問題的一般過程是建立G-結構的一個不變數系統使得足以確定一對G-結構是否為局部等價。

G-結構的聯絡

設Q是M上一個G-結構。主叢Q上的一個主聯絡誘導了任何配向量叢的一個聯絡：特別是切叢。TM以這種方式產生的線性聯絡∇ 稱為與Q相容。與Q相容的聯絡也稱為容許的聯絡。

具體說來，容許聯絡可用活動標架來理解。TM一個局部截面（即M的一個標架）定義了Q的一個截面，假設V_i是這個它的一組基。任何聯絡 ∇ 決定了一個取決於基的 1-形式 ω：

• ∇_XV_i= ω_i(X)V_j
  

這裡，作為作為 1-形式矩陣 ω ∈ Ω(M)⊗gl(n)。一個容許聯絡是 ω 在G的李代數g上的一個取值。

G-結構的撓率

任何G-結構伴隨有撓率，和聯絡的撓率有關。注意到一個給定的G-結構可能有許多不同的容許聯絡，這些聯絡可能有不同的撓率。儘管如此，我們還是能夠獨立地定義G-結構的撓率如下。

連個容許聯絡的區別是一個M上一個取值於伴隨叢Ad_Q的 1-形式。這便是說，容許聯絡的空間A是對 Ω(Ad_Q) 的一個仿射空間。

容許聯絡的撓率定義了映射

映到係數為TM中的 2-形式。這個映射是現行的；其線性化

稱為代數撓率映射。給定兩個容許聯絡 ∇ 與 ∇′，它們的撓率張量T_∇，T_∇′差一個 τ(∇−∇′)。從而T_∇在 coker(τ) 中的像與 ∇ 的選取無關。

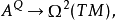
對任何一個聯絡，T_∇在 coker(τ) 中的像稱為G-結構的撓率。如果一個G-結構的撓率為 0，稱為無撓的。這恰好在Q有一個無撓容許聯絡時發生。

高階G-結構

一個特定的G-結構（例如，辛形式）上的壯觀的可積性條件可通過擴張程式處理。在這種情形，擴張後的G-結構不能構和線性標架從的一個G-子叢等價。許多情況下，擴張後它自身也是一個主叢，而其結構群可以等價於高階射流群的一個子群。此時，它也稱為一個高階G-結構（Kobayashi）。一般地，嘉當等價方法運用到這種情形。

參見

• 結構群的約化