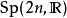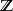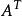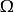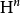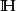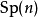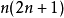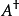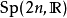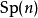基本介紹
- 中文名:辛群
- 外文名:symplectic group
- 符號:Sp(2n,F) 與 Sp(n)
- 套用學科:數學
- 定義:指涉兩類不同但關係密切的群
- 所屬領域:數學
Sp(2n, F),Sp(n),相關聯繫,
Sp(2n, F)
域F上次數為2n的辛群是由2n階辛矩陣在矩陣乘法下構成的群,記為Sp(2n,F)。由於辛矩陣之行列式恆等於一,此群是SL(2n,F)的子群。
抽象而言,辛群可定義為F上一個2n維向量空間上保存一個非退化、斜對稱雙線性形的所有可逆線性變換。帶有這種雙線性形的向量空間稱為辛向量空間。一個辛向量空間V產生的辛群記為Sp(V)。
當n=1,有Sp(2,F)=SL(2,F),當n>1時,Sp(2n,F)是SL(2n,F)的真子群。
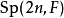
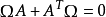
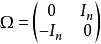
Sp(n)
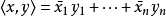
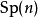


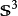
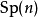
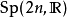
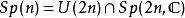
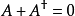
緊辛群 有時稱為酉辛群,記為
有時稱為酉辛群,記為 。
。


相關聯繫
緊緻形式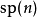 ,即
,即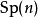 之李代數。
之李代數。
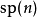
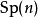
正規形式 ,即
,即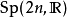 。
。

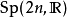
| 矩陣 | 李群 | dim/R | dim/C | 緊緻 | π1 | |
|---|---|---|---|---|---|---|
Sp(2n,R) | R | 實 | n(2n+ 1) | – | 否 | Z |
Sp(2n,C) | C | 復 | 2n(2n+ 1) | n(2n+ 1) | 否 | 1 |
Sp(n) | H | 實 | n(2n+ 1) | – | 是 | 1 |