辛空間(symplectic linear space)是一個數學術語,在數學上,辛空間是一類有特殊結構的向量空間。設V是特徵≠2的域K上的向量空間,ω是V上一個反對稱2形式。若ker ω={0},則稱ω為V上的一個辛形式。此時,(V,ω)就稱為辛空間。V是偶數維的。
基本介紹
- 中文名:辛空間
- 外文名:symplectic linear space
- 領域:數學
- 本質:向量空間
- 矩陣類型:格拉姆矩陣
- 同構群:辛群
線性空間
辛空間定義


辛群


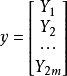

辛空間(symplectic linear space)是一個數學術語,在數學上,辛空間是一類有特殊結構的向量空間。設V是特徵≠2的域K上的向量空間,ω是V上一個反對稱2形式。若ker ω={0},則稱ω為V上的一個辛形式。此時,(V,ω)就稱為辛空間。V是偶數維的。




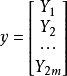

辛空間(symplectic linear space)是一個數學術語,在數學上,辛空間是一類有特殊結構的向量空間。設V是特徵≠2的域K上的向量空間,ω是V上一個反對稱2形式。若ker...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
辛算法的基礎是辛空間、辛變換,類型是矩陣。...... 辛算法對於拋物型和雙曲型偏微分方程有著廣闊的套用前景[1-2].然而辛空間、辛變換及其相應的辛矩陣等是辛計...
設V是辛空間,ψ是V上的線性變換,且g(ψ(x),ψ(y))=g(x,y)對任意的x,y∈V成立,則稱ψ是V上的辛變換。...
《波動方程的高頻近似與辛幾何》是李世雄所著的一本圖書,由科學出版社於2001-03-01出版。...
正交群是一類重要的典型群。在實數域的特殊情形,全體n×n正交方陣在矩陣乘法下構成的群稱為n次正交群,記為O(n)。一般地,設V是域K上n維列向量空間,Q(x)=...
一般線性群亦稱全線性群。一類重要的典型群。若V是體K上n維右線性空間,則V上全體可逆線性變換在映射的乘法下構成一個群,稱為V上的一般線性群或全線性群,記為...
哈密頓力學與拉格朗日力學不同的是前者可以使用辛空間而不依賴於拉格朗日力學表述。 [1] 適合用哈密頓力學表述的動力系統稱為哈密頓系統。...
辛群是一類重要的群。辛空間的自同構群。設(V,ω)是一辛空間,若φ:V→V是線性同構且滿足ω(φX,φY)=ω(X,Y),X,Y∈V,則稱φ為(V,ω)的一個自...
《矩陣論》是2013年清華大學出版社出版圖書。本書比較全面、系統地介紹了矩陣的基本理論、方法及其套用。全書分上、下兩篇,共10章,分別介紹了線性空間與線性運算元,...
