設V是辛空間,ψ是V上的線性變換,且g(ψ(x),ψ(y))=g(x,y)對任意的x,y∈V成立,則稱ψ是V上的辛變換。
基本介紹
- 中文名:辛變換
- 外文名:symplectic transformation
- 所屬學科:數理科學
- 相關概念:辛空間、辛矩陣等
定義介紹





性質定理
定理1

性質







辛矩陣
定理2
定理3




本徵值
定理4
定理5






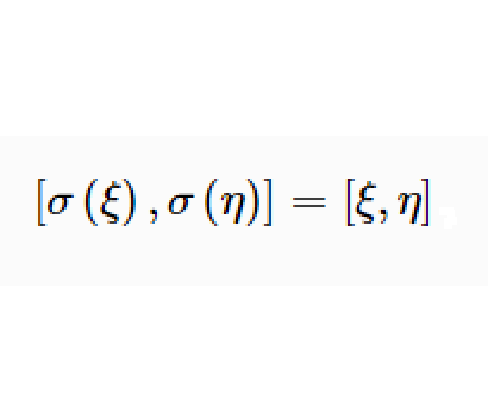
設V是辛空間,ψ是V上的線性變換,且g(ψ(x),ψ(y))=g(x,y)對任意的x,y∈V成立,則稱ψ是V上的辛變換。























設V是辛空間,ψ是V上的線性變換,且g(ψ(x),ψ(y))=g(x,y)對任意的x,y∈V成立,則稱ψ是V上的辛變換。...
數學中,一個辛矢量空間是帶有辛形式 ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
辛算法的基礎是辛空間、辛變換,類型是矩陣。...... 辛算法對於拋物型和雙曲型偏微分方程有著廣闊的套用前景[1-2].然而辛空間、辛變換及其相應的辛矩陣等是辛計...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
哈密頓系統的的正則方程在辛變換下形式不變,辛算法是基於哈密頓力學的基本原理而提出的保哈密頓系統的差分法,它使離散化後的差分方程保持原有的系統的辛結構。...
在數學與物理學中,辛向量場(symplectic vector field)是流保持辛形式的向量場。...... 這不同於下面將介紹的辛矩陣,辛矩陣表示空間的一個辛變換。如果V是有限維...
《量子力學表象與變換論:狄拉克符號法進展(第2版)》對狄拉克創立的表述量子論的符號法推陳出新,系統地建立了“有序算符內的積分(IWOP)技術”的理論,在更深層...
第10章辛空間與辛變換簡介37110.1反對稱雙線性函式與辛空間37210.1.1反對稱雙線性函式37210.1.2線性函式的外積37210.1.3辛空間的定義373...
下冊內容包括一元和多元多項式環,環和域的概念;域上的線性空間,線性映射(包括線性變換和線性函式);具有度量的線性空間(歐幾里得空間、酉空間、正交空間和辛變換)...
下冊內容包括一元和多元多項式環,環和域的概念;域上的線性空間,線性映射(包括線性變換和線性函式);具有度量的線性空間(歐幾里得空間、酉空間、正交空間和辛變換)...
