體積形式

數學中，體積形式提供了函式在不同坐標系（比如球坐標和圓柱坐標）下對體積積分的一種工具。更一般地，一個體積元是流形上一個測度。

在一個定向n-維流形上，體積元典型地由體積形式生成，所謂體積元是一個處處非零的n-階微分形式。一個流形具有體積形式若且唯若它是可定向的，而可定向流形有無窮多個體積形式（細節見下）。

有一個推廣的偽體積形式概念，對無論可否定向的流形都存在。

許多類型的流形有典範的（偽）體積形式，因為它們有額外的結構保證可選取一個更好的體積形式。在復情形，一個帶有全純體積形式的凱勒流形是卡拉比-丘流形。

基本介紹

• 中文名：體積形式
• 分類：數理科學

定義

流形M上一個體積形式是處處非0的最高階（n-維流形上的n-形式）微分形式。

用線叢的語言來說，稱最高階外積為行列式線叢，n-形式是它的截面。

對不可定向流形，一個體積“偽”形式，也稱為“奇”或“扭曲”的體積形式，可以定義為定向叢的一個處處非0截面；這個定義同樣適用於定向流形。在這種看法下，（非扭曲的）微分形式就是“偶”n-形式。除非特別地討論扭曲形式時，我們總是略去形容詞“偶”。

第一次明確地引入扭曲微分形式是德拉姆。

定向

一個流形具有體積形式若且唯若它可定向，這也可以作為可定向的一個定義。

在G-結構的語言中，一個體積形式是一個SL-結構。因為是形變收縮（因為，這裡正實數視為純量矩陣），一個流形具有一個SL-結構若且唯若具有一個-結構，即是一個定向。

線上叢的語言中，行列式叢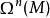的平凡性等價於可定向性，而一個線叢是平凡的若且唯若它有一個處處非0的截面，這樣又得到，體積形式的存在性等價於可定向性。

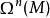
對於偽體積形式，一個偽體積形式是一個-結構，因為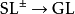 同倫等價（事實上是形變收縮），任何流形都有偽體積形式。類似地，定向叢總是平凡的，所以任何流形都有一個偽體積形式。

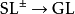
和測度的關係

任何流形有一個偽體積形式，因為定向叢（作為線叢）是平凡的。給定一個定向流形上的體積形式ω，密度 |ω| 是忘掉定向結構的非定向流形的一個偽體積形式。

任何偽體積形式ω（從而任何體積形式亦然）定義了一個波萊爾集合上一個測度：

注意區別，在於任何一個測度可以在（Borel）子集上積分，而一個體積形式只能在一個“定向”胞腔上積分。在單變數微積分中，寫成，將視為體積形式而不是測度，表明“在上沿著定向相反的反向積分”，有時記成。

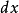
進一步，一般的測度不必連續或光滑，他們不必由體積形式定義；或更形式地說，關於一個體積形式的Radon-Nikodym導數不必絕對連續。

例子

李群

任何李群，可以由平移定義一個自然的體積形式。這就是說，如果ωe是中一個元素，那么一個左不變形式可以定義為，這裡Lg為左平移。作為一個推論，任何李群都是可定向的。這個體積形式在相差一個常數的意義下是惟一的，相應的測度稱為哈爾測度。

辛流形

任何辛流形（或更確切地為殆辛流形）有一個自然的體積形式。如果M是一個帶有辛形式ω的2n-維流形，那么由辛形式非退化可知ω處處非零。作為一個推論，任何辛流形是可定向的（事實上，已經定向）。

黎曼體積形式

任何黎曼流形（或偽黎曼流形）有一個自然的體積（或偽體積）形式。在局部坐標系下，能寫成表達式：

這裡流形為n-維，是流形上度量張量行列式的絕對值，{\displaystyle dx^{i}}為組成流形餘切叢一組基的1形式。

這個體積形式有許多不同的記號，包括：

這裡∗是霍奇對偶，從而最後一個形式∗(1)強調體積形式是流形上常數映射的霍奇對偶。

儘管希臘字母ω經常用於表示體積形式，但是這個記法很難通用，符號ω在微分幾何中經常有其它意思（比如辛形式），所以一個公式中的ω不一定就表示體積形式。

一個流形如果既是辛的又是黎曼的，如果流形是凱勒的那種方式定義的體積形式相等。