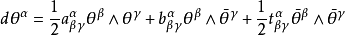殆復結構，也稱近復結構，它是殆複流形上的一種特殊結構。殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有殆復結構是一個流形是殆複流形的必要不充分條件。每一個複流形都是一個殆複流形，殆複流形在辛幾何中有重要套用。殆複流形這個概念是在20世紀40年代由Ehresmann和Hopf提出的。
基本介紹
- 中文名：殆復結構
- 外文名：almost complex structure
- 別名：近復結構
- 所屬學科：現代微分幾何
- 提出者：Ehresmann和Hopf
- 提出時間：20世紀40年代
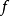
簡介,數學定義,性質,殆復結構的撓率張量,
簡介
殆復結構(almost complex structure)亦稱近復結構.流形上的一種特殊結構.
數學定義
2
維實
流形
上若有(1,1)型張量
，使任取
，
為的
點的切空間
上的線性同構，且
，則
稱為殆復結構，而
稱為殆複流形。
性質
1 殆複流形必是偶數維的可定向流形.但是，偶數維和可定向的條件並不足以保證流形有殆復結構.例如，埃雷斯曼(Ehresmann, C.)和霍普夫(Hopf , H.)證明了四維球夕不能有殆復結構.
2 每一個殆複流形M都是可定向的；
3 每個複流形都是一個殆複流形，但是具有殆復結構的微分流形並不一定是複流形；
4 若
和
分別表示
和
上的自然殆復結構，從到上的光滑映射
保持殆復結構的充分必要條件為:
殆復結構的撓率張量
在每一點
是餘切空間
的一個基，二次外形式
其中
上式又可寫成
當殆復結構的撓率為0，便說殆復結構是可積的。
定理1：在一個實解析的
維流形
上，為了殆復結構是一個複流形的自然復結構，充分必要條件是殆復結構的撓率等於零。
定理2：為了上一個殆復結構
沒有撓率，充分必要條件為對於任何局部矢量場
有
