殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有這種復結構是一個流形是殆複流形的必要不充分條件。每一個複流形都是一個殆複流形,殆複流形在辛幾何中有重要套用。殆複流形這個概念是在20世紀40年代由Ehresmann和Hopf提出的。
基本介紹
- 中文名:殆複流形
- 外文名:almost complex manifold
- 所屬學科:數學
- 提出時間:20世紀40年代
- 提出者:Ehresmann 和 Hopf
- 數學分支:微分幾何
數學定義










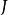

數學性質







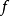
殆復結構的撓率張量


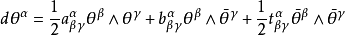




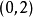



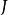


殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有這種復結構是一個流形是殆複流形的必要不充分條件。每一個複流形都是一個殆複流形,殆複流形在辛幾何中有重要套用。殆複流形這個概念是在20世紀40年代由Ehresmann和Hopf提出的。










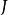








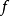


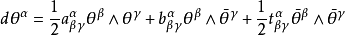




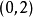



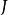


殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有這種復結構是一個流形是殆複流形的必要不充分條件。每一個複流形都是一個...
克勒流形是一類重要的複流形,具有克勒度量的複流形稱為克勒流形。例如,Cn中有界域關於伯格曼度量為克勒流形。...
殆復結構,也稱近復結構,它是殆複流形上的一種特殊結構。殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有殆復結構是一個流...
齊性複流形(homogeneous complex manifold)復的齊性流形.以H(M)表示複流形M的全純變換群.若有實李群G}H(M)可遞地作用於M上,則稱M為齊性複流形,並稱M...
埃爾米特度量(Hermite metric)是殆複流形上的一種度量。設M是殆複流形,具有殆復結構J。若M上黎曼度量g滿足g(JX,JY)=g(X,Y),這裡X,Y是M上任意向量場,...
克勒度量是特殊的埃爾米特度量。設M是具有殆復結構J的殆複流形,g為M上的埃爾米特度量,Φ是相應的克勒形式,若Φ是閉的,即dΦ=0,則稱g為克勒度量。中文...
可積性條件(integrability condition)亦稱牛朗特一尼倫伯格定理.判斷殆複流形是複流形的準則.複流形自然是一個殆複流形,反之不然.可積性條件是判斷殆複流形上...
王佳:西南大學數學統計學院教授。主要從事幾何學(微積分幾何、距離幾何)方面的研究,在殆複流形、幾何不等式的研究中取得一些成果。...
特別地,它是一個黎曼流形、複流形以及辛流形,這三個結構兩兩相容。這個三位一體結構對應於將酉群表示為一個交集:若沒有任何可積性條件,類似的概念是一個殆...
克勒形式(Kahler form)亦稱基本2形式.殆複流形上的一個特殊二次外形式.若M是具有殆復結構J和埃爾米特度量g的殆複流形,可定義2次微分式}:}CX,Y)=g(X,JY...
M上一個體積形式確定了M上一個 SLn(R)-結構。 一個2n-維辛流形有一個自然的 Sp2n(R)-結構。 一個2n-維復或殆複流形有一個自然的 GLn(C)-結構。在...
設M是具有殆復結構J的殆複流形,g為M上的埃爾米特度量,中是相應的克勒形式,若中是閉的,即d}=0,則稱g為克勒度量.給定克勒度量的複流形,就稱為克勒流形....
設M是具有殆復結構J的殆複流形,g為M上的埃爾米特度量,Φ是相應的克勒形式,若Φ是閉的,即dΦ=0,則稱g為克勒度量。給定克勒度量的複流形,就稱為克勒流形...
