埃爾米特度量(Hermite metric)是殆複流形上的一種度量。設M是殆複流形,具有殆復結構J。若M上黎曼度量g滿足g(JX,JY)=g(X,Y),這裡X,Y是M上任意向量場,則g稱為M上的埃爾米特度量。
基本介紹
- 中文名:埃爾米特度量
- 外文名:Hermite metric
- 領域:數學
- 性質:度量
- 對象:殆複流形
- 提出者:埃爾米特
殆複流形
微分流形
度量



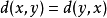

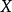

埃爾米特度量(Hermite metric)是殆複流形上的一種度量。設M是殆複流形,具有殆復結構J。若M上黎曼度量g滿足g(JX,JY)=g(X,Y),這裡X,Y是M上任意向量場,則g稱為M上的埃爾米特度量。



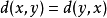

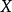

埃爾米特度量(Hermite metric)是殆複流形上的一種度量。設M是殆複流形,具有殆復結構J。若M上黎曼度量g滿足g(JX,JY)=g(X,Y),這裡X,Y是M上任意向量場,...
埃爾米特度f空jet (Hermitian metric space)一類線性空間.指帶非退化埃爾米特函式的線性空間。...
伯格曼度量(Bergman metric)由伯格曼核函式誘導的克勒度量。伯格曼核函式和伯格曼度量是研究有界域的幾何性質及函式論性質的基本工具之一。克勒度量是特殊的埃爾米特...
埃爾米特流形是一類重要的複流形,具有埃爾米特度量的複流形稱為埃爾米特流形。...... 埃爾米特流形是一類重要的複流形,具有埃爾米特度量的複流形稱為埃爾米特流...
對稱埃爾米特流形是一類重要的複流形。多複變函數論中第一個系統的分類工作是嘉當(Cartan,E)給出的,他給出了對稱埃爾米特空間在全純等價下的分類。...
帶有一個埃爾米特度量的流形是殆埃爾米特流形;凱勒流形是帶有滿足一個可積性條件的埃爾米特度量的流形,它有多種等價的表述。凱勒流形可以多種方法刻畫:它們通常...
設M有埃爾米特度量h,它對應一個(1,1)型外微分形式 稱為h的伴隨克勒形式。當dw=0時,h稱為克勒度量。具有克勒度量的複流形稱為克勒流形。...
任何複流形上總存在埃爾米特度量,它是一種復形式的黎曼度量.具有埃爾米特度量的複流形稱為埃爾米特流形.在埃爾米特流形上可構造一個2次外微分形式,稱為克勒形式...
中。設ω上給定埃爾米特度量,取 在 中的正交補作為點 上的纖維,得以 為底空間的復n-1維向量叢 ,則陳類 按ω的復維數遞推地定義為:頂陳類(即最高維陳...
中,設ω 上給定埃爾米特度量,取 v 在 中的正交補作為點 v 上的纖維,得以 為底空間的復 n-1 維向量叢 ,則陳類 按ω 的復維數遞推地定義為:頂陳類(...
中,設ω 上給定埃爾米特度量,取 v 在 中的正交補作為點 v 上的纖維,得以 為底空間的復 n-1 維向量叢 ,則陳類 按ω 的復維數遞推地定義為:頂陳類(...
3.復歐氏空間C'",若賦予它通常的埃爾米特度量,則C’成為一個全純截曲率為。的完備、單連通復空間.任何m維復空間形式(度量乘以適當的常數)必局部復解析等距於...
帶有一個埃爾米特度量的流形是殆埃爾米特流形;凱勒流形是帶有滿足一個可積性條件的埃爾米特度量的流形,它有多種等價的表述。凱勒流形可以多種方法刻畫:它們通常...
