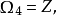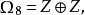兩個k維閉微分流形V,W稱為配邊,如果V,W一起構成(n+1)維有邊緣流形的邊緣。這個非常明顯的概念首先是托姆在1954年的論文中提出來的。托姆對一般流形建立配邊理論,對微分流形進行最粗的分類之後,流形的分類可以分兩個方向進行:一是對於一般流形進行較為精細的分類,另一是沿著配邊理論的方向,對更特殊類的流形做更為細緻的分類。這後一方向,從托姆時起一直仿照著托姆的模式繼續進行並取得重要的成就。到現在已經對20多種配邊理論進行過研究。配邊理論還有復配邊理論、辛配邊理論等,它們各有一些結果。
基本介紹
- 中文名:配邊理論
- 外文名:cobordism theory
- 所屬學科:數學
- 所屬問題:微分拓撲學
- 相關概念:配邊,閉微分流形,定向配邊類等
- 創立者:托姆
基本介紹,無定向配邊理論,定向配邊理論,托姆基本定理,結構定理,定向配邊不變數,
基本介紹
配邊理論從直觀上十分清楚。兩個k維閉微分流形V,W稱為配邊,如果V,W一起構成(n+1)維有邊緣流形的邊緣。
這個非常明顯的概念首先是托姆在1954年的論文中提出來的。這篇劃時代的論文題目是“微分流形的某些整體性質”,實際上完成了流形在配邊這個等價關係下的分類,在先不考慮定向的情況下,每一維的所有流形都可以根據它們是否配邊來歸類,相互配邊的流形算作同一類。托姆創立了配邊理論,他指出任何兩個流形屬於同一類的充分必要條件,從而完成了流形的粗分類的工作,然後他又對每一類找出一個代表,有了這些代表,任何一個流形就屬於某一個代表的類了。
在托姆之前,數學家也曾考慮類似的問題。蘇聯數學家龐特里亞金和羅赫林,都曾經研究過更基本的問題:什麼時候一個k維流形是一個(k+1)維流形的邊緣?由於同調論的關鍵部分是邊緣運算元,因此他們把這種問題稱為內在同調。這樣的問題顯然只是配邊理論的一個特殊情形,而且產生不出配邊等價類的結構,也出現不了微分流形的粗分類。從這種情形下看也可以看出托姆思想的偉大創造性。托姆的配邊理論還有另外一個來源,就是一個微分流形的同調類能否被其子流形來表示。這是著名的斯廷洛德問題。托姆在他的研究中也給這個問題一個明確的回答:
可實現性定理 流形 的同調類
的同調類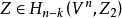 能用子流形來實現的充分必要條件是存在一個映射
能用子流形來實現的充分必要條件是存在一個映射

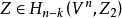
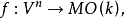
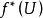
這裡的 是以正交群
是以正交群 為結構群的萬有k維向量叢
為結構群的萬有k維向量叢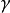 的托姆複合形,而流形X上一個向量空間叢
的托姆複合形,而流形X上一個向量空間叢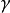 的托姆複合形,就是把與
的托姆複合形,就是把與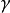 相伴的k維閉圓盤叢
相伴的k維閉圓盤叢 中把其邊緣所構成的(k-1)維球面叢
中把其邊緣所構成的(k-1)維球面叢 縮為一點後所成的空間,這個空間稱為托姆空間,由於它有CW複合形的同倫型,因此稱為
縮為一點後所成的空間,這個空間稱為托姆空間,由於它有CW複合形的同倫型,因此稱為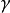 的托姆複合形。而
的托姆複合形。而


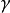
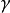
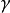


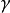


無定向配邊理論
托姆在所有不考慮定向的流形中,引入一個等價關係,其相互配邊的流形(同一維)構成一個等價類。n維閉流形等價類全體在加法之下構成阿貝爾群 ,其中加法為
,其中加法為




托姆的工作完整地定出配邊環的結構,他證明了下列結果:
(1)托姆基本定理


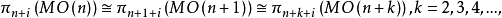
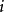
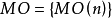
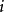
(2)n的結構定理
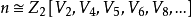
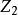

成元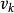 ,且每
,且每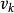 為實射影空間
為實射影空間 的配邊類。
的配邊類。
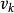
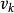

(3)配邊的充分必要條件 兩流形配邊若且唯若其每個施蒂費爾-惠特尼示性數對應相等。
定向配邊理論
定向配邊理論的研究對象是所有定向流形的集合,其中所有流形都有兩種定向。如果一種用 表示,另一種則用
表示,另一種則用 表示,它們在這個集合中代表不同的元素。
表示,它們在這個集合中代表不同的元素。


兩個 維閉流形
維閉流形 稱為定向配邊,如果存在一個
稱為定向配邊,如果存在一個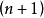 維可定向有邊緣流形X,使得
維可定向有邊緣流形X,使得


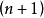



經過托姆、米爾諾(Milnor,John Willard,1931-) 和沃爾的研究, 的結構也完全決定。
的結構也完全決定。

托姆基本定理


結構定理





1960年,米爾諾證明 沒有p分量,p為任意奇素數。同年,沃爾證明
沒有p分量,p為任意奇素數。同年,沃爾證明 的2分量中不含4階元素。
的2分量中不含4階元素。


設 為
為 中所有撓元構成的理想,則
中所有撓元構成的理想,則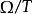 為
為 上多面式環,以
上多面式環,以 為生成元,其中
為生成元,其中 可取為復
可取為復 維非奇異代數簇。
維非奇異代數簇。


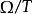




定向配邊不變數
兩個定向閉流形定向配邊若且唯若其所有的施蒂費爾-惠特尼示性數和龐特里亞金示性數對應相等。