無定向配邊類

無定向配邊類(unoriented cobordism class)又稱未定向配邊類，是流形的一種等價類，邊緣流形的理論稱為配邊，兩個緊n維流形屬於一個配邊類，如果它們的不交並是個邊緣， 可以證明這是一種等價關係。兩個光滑閉n維流形M₁與M₂屬於同一個無定向的配邊類的充分必要條件是它們的不相交的並M₁∪M₂是光滑緊n+1維流形的邊緣。

基本介紹

• 中文名：無定向配邊類
• 外文名：unoriented cobordism class
• 別稱：未定向配邊類
• 屬性：流形的一種等價類
• 相關概念：配邊，配邊理論等

基本介紹

未定向配邊類是流形的一種等價類，兩個光滑閉n維流形M₁與M₂屬於同一個無定向的配邊類的充分必要條件是它們的不相交的並M₁∪M₂是光滑緊n+1維流形的邊緣。

無定向配邊理論

托姆在所有不考慮定向的流形中，引入一個等價關係，其相互配邊的流形(同一維)構成一個等價類。n維閉流形等價類全體在加法之下構成阿貝爾群，其中加法為

么元(零元)就是本身是邊緣的流形，而且兩流形的拓撲積可定義乘法

於是直和

成為分次交換環(代數)，稱為配邊環或托姆代數。

相關概念

定向配邊類

定向配邊類(oriented cobordism class)是流形的一種等價類，對於兩個光滑緊定向n維流形M與M′，若存在一個光滑緊的帶邊的定向流形X，使得∂X及其誘導定向在保持定向的同胚之下同胚於M與(-M′)的無交並，則稱M與M′屬於同一個定向配邊類。

定向配邊類的這種關係是自反的、對稱的和傳遞的，因此是一個等價關係，在這種等價關係之下的等價類之集記為Ω_n，對Ω_n中的任意兩個元素{M}，{M′}，用無交並作為群運算，則Ω_n構成一個阿貝爾群，這個群的零元就是空流形的配邊類。例如，可以列出定向配邊類群如下：Ω₀≅Z，Ω₁=0，Ω₂=0，Ω₃=0，Ω₄≅Z，Ω₅=Z/2，Ω₆=0，Ω₇=0，Ω₈≅Z⊕Z，Ω₉=(Z/2)⊕(Z/2)，Ω₁₀≅Z/2，Ω₁₁≅Z/2。

配邊理論

兩個緊緻的無邊的n維C^∞流形M₀和M₁，稱為是模2配邊的，如果存在緊緻帶邊的n+1維C^∞流形W，使∂WC^∞微分同胚於M₀×{0} ∪M₁×{1}，記作M0～M₁。模2配邊是n維緊緻無邊流形之間的一個等價關係。n維C^∞流形M所在的等價類記作[M]₂，等價類的全體作成的集合記作ℛⁿ，稱為n維不定向的配邊群。

類似地，M₀和M₁是定向的n維無邊C^∞流形，它們的定向分別為ω₀和ω₁，稱(M₀，ω₀)和(M₁，ω₁)是配邊的，如果存在n+1維帶邊C^∞流形(W，θ)及保持定向的C^∞微分同胚f：(∂W，∂θ)→(M₀×{0}，-ω₀)∪ (M₁×{1}，ω₁)。n維定向無邊定向C^∞流形的等價類的全體做成的集合記作Ωⁿ。

把W嵌入到某歐氏空間Rq，可定義[M0]₂+ [M₁]₂等於[M0+M₁]₂，不難證明ℛⁿ對加法做成一個交換群稱為n維配邊群。對加法和乘法做成一個有單位元的交換環，稱為n維配邊環。且更有甚者，做成一個模2的交換代數，稱為托姆(Thom)代數。

類似地在Ωⁿ中定義加法和乘法，則Ωⁿ對加法做成交換群，稱為n維定向配邊群，對加法和乘法做成有單位元的環，稱為n維定向配邊環。

拓撲流形的定向

拓撲流形的定向(orientation of topological manifold)是確定流形指向的方式問題，有多種等價的方式來定義流形的定向，這裡介紹比較基本的兩種。設M為n維拓撲流形，由定義可知存在M的一個開覆蓋{U_λ|λ∈Λ}，使得對於每個U_λ有同胚φ_λ：U_λ≌Rⁿ(或 )，於是當U_λ∩U_μ≠∅時，

是Rⁿ(或 )的開子集之間的同胚，若在M上可選取U_λ與φ_λ，λ∈Λ，使得當U_λ∩U_μ≠∅時， 總是保向同胚，則稱M為可定向流形；否則，稱為不可定向流形。

設 為單位區間， 為流形M的一條道路，選取 的一個分割

使得 某 ，現在通過 選取 的序向，使得在 和 上，它們有一致的序向，則當a為環道時，有a(0)的鄰域 到a(1)的鄰域 的一個同胚h，若h為保向同胚，則稱a為保向的；否則稱a為逆向的，於是M可定向的等價說法是：M上的任意環道都是保向環道，由於具有相同基點的同倫環道有相同的保向性，所以單連通流形必定可定向，因此n維球面Sn當n≥2時可定向(當然圓周S1也可定向)，另一方面，如圖所示，默比烏斯帶的腰圓是一條逆向曲線，從而默比烏斯帶不可定向，因此一切包含默比烏斯帶的曲面均不可定向，所以2維實射影平面、克萊因瓶等均為不可定向的閉曲面(2維流形)。

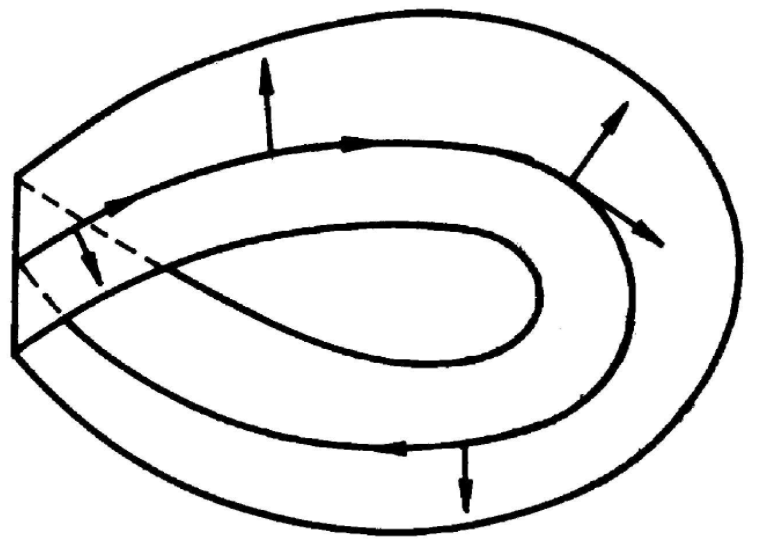圖1