斯托克斯理論,是微分幾何中關於微分形式的積分的定理,因為維數跟空間的不同而有不同的表現形式,它的一般形式包含了向量分析的幾個定理,以斯托克斯爵士命名。
基本介紹
- 中文名:斯托克斯理論
- 外文名:Stokes theory
- 學科:測繪科學
三維平面上的斯托克斯公式,流形上的斯托克斯公式,
三維平面上的斯托克斯公式
設S是分片光滑的有向曲面,S的邊界為有向閉曲線Γ,即 ,且Γ的正向與S的側符合右手規則: 函式P(x,y,z)、Q(x,y,z)、R(x,y,z)都是定義在“曲面S連同其邊界Γ”上且都具有一階連續偏導數的函式,則有:
,且Γ的正向與S的側符合右手規則: 函式P(x,y,z)、Q(x,y,z)、R(x,y,z)都是定義在“曲面S連同其邊界Γ”上且都具有一階連續偏導數的函式,則有:

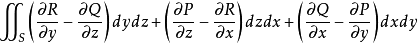

引進符號行列式,這個公式也可以寫成以下形式:


它將三維 空間上“向量場的旋度的曲面積分”跟“向量場在曲面邊界上的線積分”之間建立聯繫,這是一般的斯托克斯公式(在 n=2 時)的特例,我們只需用ℝ3 空間上的內積把向量場看作等價的1-形式。該定理的第一個已知的書面形式由威廉·湯姆森(開爾文勳爵)給出,出現在他給斯托克斯的信中。
類似的,高斯散度定理

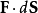
流形上的斯托克斯公式
令 M 為一個可定向分段光滑 n 維流形,令 ω 為 M 上的 n−1 階 C 類緊支撐微分形式。如果 ∂M 表示 M 的邊界,並以 M 的方向誘導的方向為邊界的方向,則
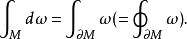
這裡 dω 是 ω 的外微分, 只用流形的結構定義。這個公式被稱為一般的斯托克斯公式(generalized Stokes' formula),它被認為是微積分基本定理、格林公式、高-奧公式、三維空間上的斯托克斯公式的推廣;後者實際上是前者的簡單推論。
該定理經常用於 M 是嵌入到某個定義了 ω 的更大的流形中的子流形的情形。
定理可以簡單的推廣到分段光滑的子流形的線性組合上。斯托克斯定理表明相差一個恰當形式的閉形式在相差一個邊界的鏈上的積分相同。這就是同調群和德拉姆上同調可以配對的基礎。