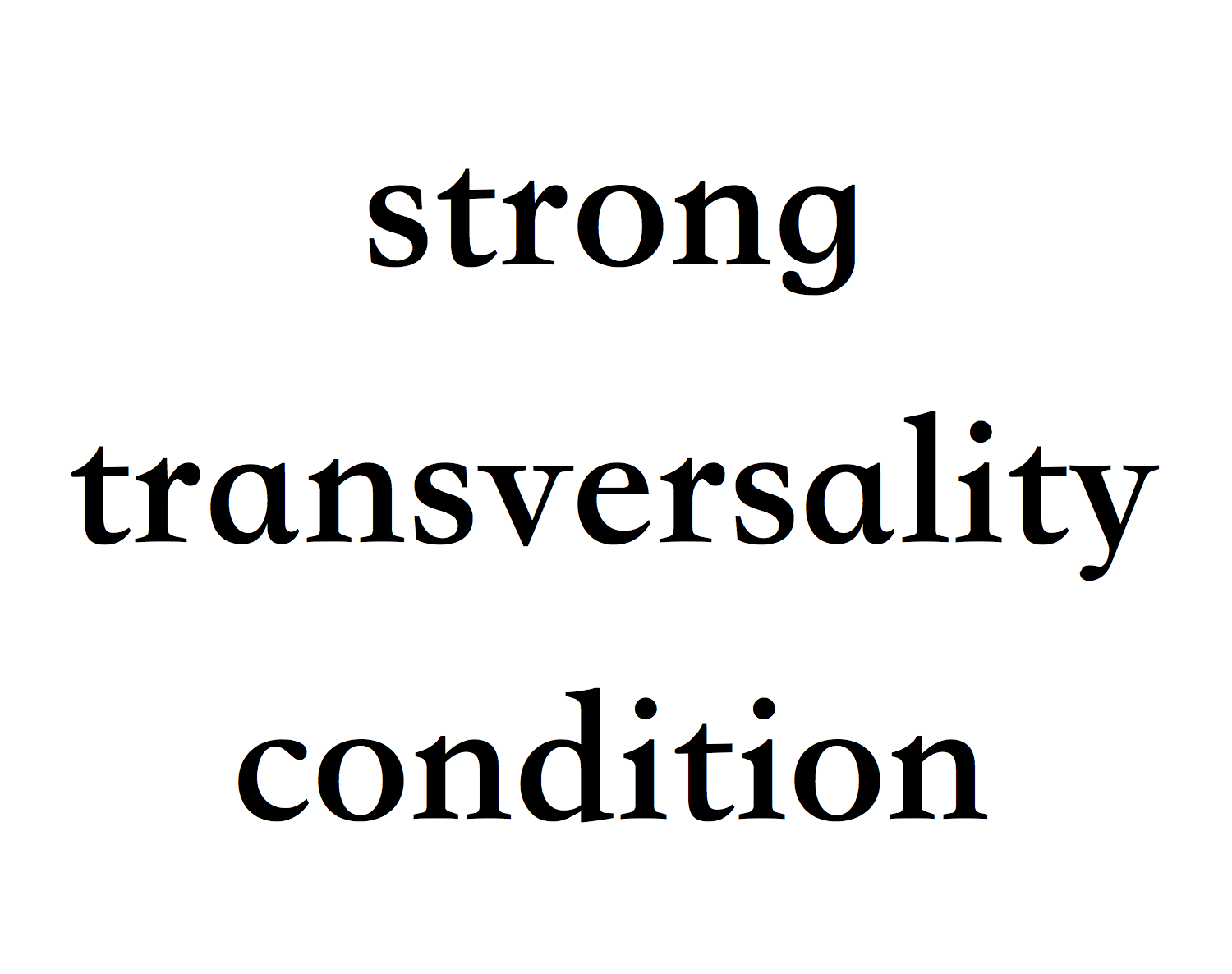強橫截條件亦稱幾何式橫截條件，結構穩定系統的基本條件之一。微分動力系統的研究指出：若系統滿足公理 A 和強橫截條件，則系統是結構穩定的。人們通常把這類系統稱為是公理A結構穩定系統。現已得到對微分同胚和向量場，結構穩定系統等價於公理A結構穩定系統。
基本介紹
- 中文名：強橫截條件
- 外文名：strong transversality condition
- 適用範圍：數理科學
簡介,公理A,
簡介
強橫截條件是在公理 A 條件下為保證結構穩定性而進一步提出的一個條件。這個概念在流和離散系統中形式上平行地出現，這裡就離散情形加以說明。在公理 A 條件下，流形 M 的每個點正向都趨向某個基本集，實際上與基本集中的某個點正向漸近，即共處於同一穩定流形之中。負向也如此。因此，在公理 A 條件下，M 的每個點x 的穩定流形 Ws(x) 和不穩定流形Wu(x)都是可微的浸入子流形。
如果對任意兩點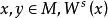
和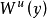
作為可微子流形橫截相交，稱一個公理 A 微分同胚滿足強橫截條件。
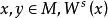
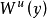
羅賓(J.Robbin) 和魯賓遜(R.C.Robinson) 證明，一個微分同胚如果滿足公理 A 和強橫截條件，則是結構穩定的。這是20世紀70年代微分動力系統的一個主要成果。
公理A
這是斯梅爾為刻畫結構穩定性提出的一種關於非遊蕩集的條件。這個概念在流和離散系統中形式上平行地出現，但由於基礎是雙曲集的概念，實際上蘊涵著重要的不同。這裡就離散情形加以說明。
一個微分同胚的動力性態主要體現在非遊蕩集上，或更大一點，鏈回歸集上。至於遊蕩部分，或非鏈回歸部分，則比較簡單。鏈回歸分解為互不相交的、不可分解的緊不變集，稱為鏈傳遞分支。一個鏈傳遞分支本身可能有複雜的動力形態。但造成動力形態高度複雜的一個更為嚴重的原因是，一個微分同胚可能有，甚至可能在擾動下持續地有，無窮多個鏈傳遞分支。
相比之下，公理 A 微分同胚由於只有有限個鏈傳遞分支，動力形態就相對簡單（即使各個鏈傳遞分支內部可能有斯梅爾馬蹄那樣的複雜程度）。如果把馬蹄這樣的不變集看成是一個複雜化了的“鞍點”，把雙曲吸引子和排斥子看成是一個複雜化了的“匯點”和“源點”，那么公理 A 微分同胚就在更高的複雜度下類比於一個莫爾斯-斯梅爾微分同胚。
在公理 A 的條件基礎上，再加上無環條件或強橫截條件，就是斯梅爾提出的、後來被證明為Ω 穩定和結構穩定的充分條件。
