基本介紹
- 中文名:雙曲不變集
- 外文名:hyperbolic invariant set
- 領域:數學
- 定義:雙曲周期點的推廣
- 系統:微分動力系統
- 對象:黎曼流形
概念
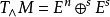
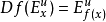





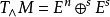
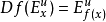





雙曲周期點又稱雙曲不動點,是可微映射具有局部結構穩定性質的不動點。雙曲不變集(hyperbolic invariant set)雙曲周期點概念的推廣,是微分動力系統的一個極為重要...
流雙曲不變集(hyperbolic invariant set of aflow)雙曲周期軌概念的推廣,是C'流的一個重要的不變集。...
不變集C結構穩定性(C structural stabilityof invariant set)微分動力系統研究的重要內容之一指系統經過小擾動之後,其不變集不改變其軌道結構,僅僅是不變集各點的...
基本集是動力系統研究的重要不變集之一。它是根據公理A系統譜分解的基本集所具有的動力學性質而抽象出來的概念。...
第十章雙曲不動點的穩定流形與不穩定流形1穩定集與不穩定集2穩定流形定理第十一章符號動力系統與“馬蹄”1符號動力系統2移位不變集...
統計特性在不同時刻平穩不變的一類隨機過程。數學上嚴格的平穩性概念是:一隨機...具有雙曲不變集系統的極限跟蹤性[J]. 數學年刊A輯(中文版),2004,(05):613...
無環條件(no cycle condition)是Ω穩定性的基本條件之一,描述了動力系統的不變集之間的關係。通常所說公理A系統滿足無環條件或具有無環性質是指:Ω(f)的譜分解...
微分動力系統的研究對象是微分流形M上的微分同胚φ或流 φt。有關的遍歷性研究往往涉及雙曲性條件。所謂微分同胚φ在不變集Λ上有雙曲結構,是指M的切空間叢在...
有限型子移位(subshift of finite type)亦稱雙邊拓撲馬爾可夫鏈,是符號動力系統中一個很有意義的子系統,其重要性在於它能夠作為十分重要的微分同胚某不變集的模型...
14.朱玉峻,王玲書,張金蓮,具有雙曲不變集系統的極限跟蹤性,數學年刊, 25 (5)(2004),613-620. (English version: Zhu Yujun, Wang Lingshu, Zhang Jinlian...
三維自控向量域中雙曲不動點的軌道同宿;二維時間周期向量域中同宿軌道的Melnikov方法;Liapunov指數;混沌和奇怪吸引子;雙曲不變集;局部余維中的全局分叉點-二分叉...
如果把馬蹄這樣的不變集看成是一個複雜化了的“鞍點”,把雙曲吸引子和排斥子看成是一個複雜化了的“匯點”和“源點”,那么公理 A 微分同胚就在更高的複雜...
例如,套用典範方程組可以對推廣的C1封閉引理及雙曲不變集半結構穩定性給出證明等。 [1] 參考資料 1. 《數學辭海》總編輯委員會.《數學辭海》第3卷:東南大學...
2.5 周期點的穩定性2.6 雙曲不動點的穩定流形與不穩定流形2.7 不變集與吸引子2.8 拓撲共軛與符號動力系統2.9 帳篷映射2.10 迪萬尼混沌定義第3章 拋物線映射...
