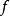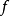若𝜙為浸入映射,同時又是單映射,則稱它為單浸入(injective immersion)。
基本介紹
- 中文名:單浸入
- 外文名:injective immersion
- 適用範圍:數理科學
簡介,浸入,定義,性質,可微映射,
簡介
浸入
浸入亦稱浸入映射,是具有某種性質的流形間的映射。
設𝜙:M→N是一個可微映射,若對於每個p∈M,𝜙∗|p為非奇異的,則稱𝜙為浸入映射,簡稱浸入。
定義
若𝜙同時又是單映射,則稱它為單浸入。
性質
浸入映射是局部單映射,但它未必是整體單映射。
可微映射
設D是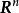 中的一個區域,
中的一個區域,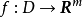 是以D為定義域的映射,
是以D為定義域的映射,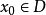 ,如果對於自變數
,如果對於自變數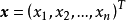 的增量
的增量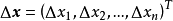 ,因變數
,因變數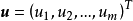 的增量
的增量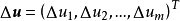 可以分解為
可以分解為
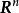
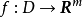
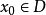
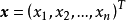
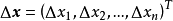
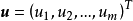
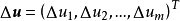
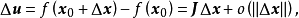
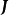
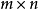
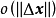
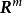
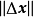
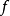
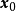
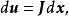

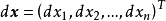
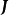
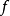
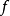
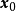
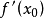
如果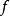 在D上的每一點處可微,則稱
在D上的每一點處可微,則稱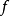 為D上的可微映射。
為D上的可微映射。