基本介紹
- 中文名:柯西中值定理
- 外文名:Cauchy mean value theorem
- 表達式:[f(b)-f(a)]/[g(b)-g(a)]=f'(ξ)/g'(ξ)
- 提出者:柯西
- 套用學科:數學
- 適用領域範圍:數學 物理學
- 套用:證明等式、不等式、求極限等
人物簡介
定理定義


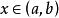




證明





幾何意義


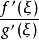
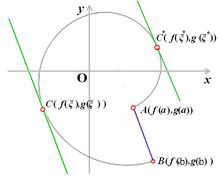
套用例子
泰勒公式







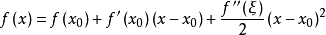







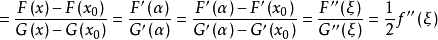
洛必達法則




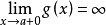


不等式








中值點






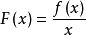







定理求極限








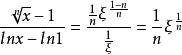











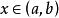











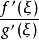








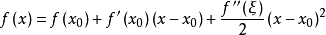







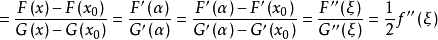




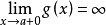
















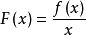















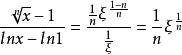








柯西中值定理是拉格朗日中值定理的推廣,是微分學的基本定理之一。其幾何意義為,用參數方程表示的曲線上至少有一點,它的切線平行於兩端點所在的弦。該定理可以視作...
中值定理是反映函式與導數之間聯繫的重要定理,也是微積分學的理論基礎,在許多方面它都有重要的作用,在進行一些公式推導與定理證明中都有很多套用。中值定理是由眾多...
拉格朗日中值定理又稱拉氏定理,是微分學中的基本定理之一,它反映了可導函式在閉區間上的整體的平均變化率與區間內某點的局部變化率的關係。拉格朗日中值定理是羅...
《微積分中值定理若干問題》由樊守芳編著,作者認為在數學研究中要注意如下幾個要點:從無到有,從易到難,由小到大,由淺入深。《微積分中值定理若干問題》就是...
拉格朗日定理存在於多個學科領域中,分別為:微積分中的拉格朗日中值定理;數論中的四平方和定理;群論中的拉格朗日定理 (群論)。...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...積分第二中值定理夾逼定理卷積定理 極值定理角平分線定理K柯西定理...
4·3 柯西中值定理 5.函式的增減 5·1 增函式·減函式 5·2 極大和極小 5·3 最大和最小 6.高階導函式及其套用 6·1 二階導函式和n階導函式 6·...
b】上連續,在開區間(α,b)內可微,則在這個區間內至少存在一點ξ,使得當g(x)=x時,上面定理與拉格朗日定理有同一形式,所以柯西中值定理是拉格朗日定理的最一般...
在柯西中值定理的證明中,也運用到了參數方程。柯西中值定理如果函式f(x)及F(x)滿足:⑴在閉區間[a,b]上連續;⑵在開區間(a,b)內可導;...
第六章 微分中值定理及其套用 1 拉格朗日定理和函式的單調性 一 羅爾定理與拉格朗日定理 二 單調函式 2 柯西中值定理和不定式極限 一 柯西中值定理 二 不定式...
1.3.3 柯西中值定理 1.3.4 等式 1.4 洛必達法則 1.4.1 □型未定式 1.4.2 □型未定式 1.5 習題1.1 1.6 泰勒展開式 1.6.1 泰勒公式 1.6.2 泰勒級...
Analytic geometry 概述 在柯西中值定理的證明中 簡介 平面解析幾何包含以下幾部分 直角坐標 有向線段 目錄 1 解析幾何簡介 2 歷史 3 基本理論 ▪ 坐...
第一節微分中值定理 一、羅爾定理 二、拉格朗日中值定理 三、柯西中值定理 第二節洛必達法則 一、0/0、∞/∞型未定式的運算 二、其他類型未定式...
這一重大價值是後來由 拉格朗日發現的,他把這一定理刻畫為微積分的基本定理。泰勒定理的嚴格證明是在定理誕生一個世紀之後,由柯西給出的。 泰勒定理開創了有限差分...
2.6 羅爾定理.拉格朗日定理和柯西定理(習題1235-1267)2.6.1 羅爾定理(習題1235-1243)2.6.2 拉格朗日中值定理(習題1244-1251)...
1 柯西中值定理與洛必達法則2 泰勒(Taylor)公式3 函式的凹凸與拐點4 不等式的證明5 函式的作圖6 方程的近似求解第九章 定積分的進一步討論...
3.1.3柯西中值定理和不定式的極限3.2函式的極值和最大值、最小值3.2.1函式的極值及其求法3.2.2函式的最大值與最小值3.3曲線的凹凸性和函式圖形的描繪...
3.1.1羅爾定理3.1.2拉格朗日中值定理3.1.3柯西中值定理3.2洛必達法則3.3函式的單調性與函式的極值3.3.1函式的單調性3.3.2函式的極值...
微分中值定理及其套用 1 拉格朗日定理和函式的單調性 一 羅爾定理與拉格朗日定理 二 單調函式 2 柯西中值定理和不定式極限 一 柯西中值定理 二 不定式極限 3 ...
第3章 微分中值定理與導數的套用 85 3.1 微分中值定理 85 3.1.1 羅爾定理 85 3.1.2 拉格朗日中值定理 86 3.1.3 柯西中值定理 88 3.1.4 泰勒公式 88 習...
習題2-5 總習題二 習題答案 第3章微分中值定理與導數的套用 3.1微分中值定理 3.1.1羅爾定理 3.1.2拉格朗日中值定理 3.1.3柯西中值定理3.1...
第四章中值定理與導數套用 4.1中值定理 4.1.1羅爾定理 4.1.2拉格朗日中值定理 4.1.3柯西中值定理 習題4.1 4.2羅比塔法則 習題4.2 4.3函式的單調性...
題型四 直接用拉格朗日中值定理或柯西中值定理證明 題型五 雙介值問題,要證存在ξ,η使G(f'(ξ),f'(η),)=0 題型六 證明存在ξ,使得f(n)(ξ)=k(k≠...
辛普森法習題3.6第三章總練習題第四章 微分中值定理與泰勒公式§1 微分中值定理習題4.1§2 柯西中值定理與洛必達法則習題4.2§3 泰勒公式§4 關於泰勒公式的余...
第六章微分中值定理及其套用第一節拉格朗日定理和函式的單調性第二節柯西中值定理和不定式極限第三節泰勒公式第四節函式的極值與最大(小)值...
第3章微分中值定理與導數的套用3.1微分中值定理3.1.1費馬引理3.1.2羅爾定理3.1.3拉格朗日中值定理3.1.4柯西中值定理習題3.13.2洛必達法則...
第3章 中值定理與導數的套用3.1 中值定理3.1.1 羅爾定理3.1.2 羅爾定理的套用3.1.3 拉格朗日中值定理3.1.4 拉格朗日中值定理的套用3.1.5 柯西中值定理...
