柯西積分公式

柯西積分公式是一把鑰匙，他開啟了許多方法與定理；他刻畫了解析函式的又一種定義；人們對它的研究極具意義，讓解析函式論能夠單獨脫離於實函式。通過柯西積分公式就可以把解析函式f(z)在簡單閉曲線C的內部任意一點處的值邊界C上的值表示。這是解析函式的又一特徵。柯西積分公式不但提供了計算某些複變函數沿閉路積分的一種方法，而且給出了解析函式的一個積分表達式，從而是研究解析函式的有力工具。

基本介紹

• 中文名：柯西積分公式
• 外文名：Cauchy Integral Formula
• 領域：解析函式
• 滿足條件：區域封閉
• 公式形式：積分
• 分類：在有界區域和無界區域

定義及證明

設 為單連通域D內的個解析函式， 為D內一點，環路C為D內包圍 的一條簡單閉曲線，由單連通

域柯西定理可知，

．

現在考慮積分

，

顯然函式 在 處不解析，所以積分 一般不為零．根據閉路變形原理，這個積分的值對圍繞 的任一簡單閉曲線都是相同的．因此，可以取以 為圓心、半徑為 的很小的圓周 作為積分曲線 ．由於 的連續性，在 上的函式 的值將隨著 的縮小而逐漸接近於它的圓心 處的值 ．我們作出這樣的猜想，積分

事實上，我們有下面的定理．

柯西積分公式: 如果 在區域D解析， 為D內一點，C為D內包圍 的任意一條正向簡單閉曲線，它的內部完全含於D，則

.

證明：由於 在點 連續，任意給定一個正的小數 ，必然存在一個 ，使得當 時， 。取 ，使正向圓周 全部在C的內部，根據閉路變形原理有

根據複變函數積分不等式，有

從而必有

於是有

相關推論

1. 中值定理

2.設 在簡單閉曲線 所圍成的復連通域D內解析，並在 上連續， 在 的內部， 為D內一點，則

積分公式

對於無界區域，需要假設 在簡單閉合圍道C上及C外（包括 點）單值解析，類似計算

其中a為C外一點，積分路徑C的走向是繞無窮遠點的正向，即順時針方向，如圖所示。在C外再作一個以原點為圓心，R為半徑的圓 ，對於C和 所包圍的復連通區域，根據有界區域的柯西積分公式，就有

的走向是逆時針方向。只要R足夠大，這個結果當然與R的具體大小無關，於是可令 ,若

可得

因此，

當 時，就得到了無界區域的柯西積分公式；如果 在簡單閉合圍道C以及C外解析，且當 時， 一致趨於0，則柯西積分公式

仍然成立，此處a為C外一點，積分路線C為順時針方向。

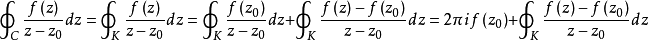
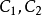
無界區域的柯西積分公式