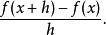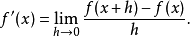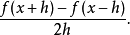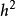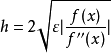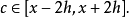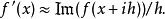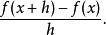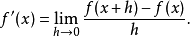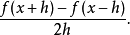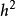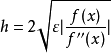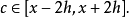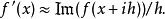基本介紹
簡介,有限差分法,利用浮點數,高階方法,微分求積,復變的方法,
簡介
數值微分(numerical differentiation)根據函式在一些離散點的函式值，推算它在某點的導數或高階導數的近似值的方法。通常用差商代替微商，或者用一個能夠近似代替該函式的較簡單的可微函式（如多項式或樣條函式等）的相應導數作為能求導數的近似值。例如一些常用的數值微分公式(如兩點公式、三點公式等)就是在等距步長情形下用插值多項式的導數作為近似值的。此外，還可以採用待定係數法建立各階導數的數值微分公式，並且用外推技術來提高所求近似值的精確度。當函式可微性不太好時，利用樣條插值進行數值微分要比多項式插值更適宜。如果離散點上的數據有不容忽視的隨機誤差，應該用曲線擬合代替函式插值，然後用擬合曲線的導數作為所求導數的近似值，這種做法可以起到減少隨機誤差的作用。數值微分公式還是微分方程數值解法的重要依據。
有限差分法
最簡單的方式是使用有限差分近似。
簡單的二點估計法是計算經過(x,f(x))及鄰近點(x+h,f(x+h))二點形成割線的斜率選擇一個小的數值h，表示x的小變化，可以是正值或是負值。其斜率為
此表示法是牛頓的差商，也稱為一階均差。
割線斜率和切線斜率有些差異，差異大約和h成正比。若h近似於0，則割線斜率近似於切線斜率。因此，函式f真正在x處真正的斜率是割線趨近切線時的差商：
若直接將h用0取代會得到除以零的結果，因此計算導數需要一些較不直覺的的方式。
同様的，切線斜率也可以用(x - h)和x二點的割線斜率近似。
另外一種二點估計法是用經過(x-h,f(x-h))和(x+h,f(x+h))二點的割線，其斜率為
上述公式稱為對稱差分，其一次項誤差相消，因此割線斜率和切線斜率的差和
成正比。對於很小的h而言這個值比單邊近似還要準確。特別的是公式雖計算x點的斜率，但不會用到函式在x點的數值。
估計誤差為：
其中c為在x-h和x+h之間的某一點。此誤差沒有包括因為有限準確度而產生的捨入誤差。
很多工程計算機都是用對稱差分來計算導數，像德州儀器（TI）的TI-82、TI-83、TI-84及TI-85，其h=0.001。
雖然在實務十分常用，但上述二種方式的數值微分常被研究者批評，尤其是被一些鼓勵使用自動微分的研究者批評，因為上述的數值微分其精確度不高，若計算器精準度是六位數，用對稱差分計算導數只有三位數的精確度，而若是找到一計算斜率的函式，仍可以有幾乎六位數的精確度。例如假設f(x) = x，用2x計算斜率有幾乎完整的準確度，而用差分近似就會有上述的問題。
利用浮點數
在浮點數運算下，不同的 h造成的捨入誤差及公式誤差，只有在特定值下誤差才是最小值
若計算時使用浮點數，就需要考慮h要取到多小。若選的太小，相減之後會有大的捨入誤差，事實上整個有限差分的公式都是病態的，若h夠小，導數不為零的情形下，在相消後會得到數值微分為零的結果，若h大小，計算割線斜率的結果就會更加準確，但用割線斜率估算切線斜率的誤差就更大了。
一種可以產生夠小的h，但又不會產生捨入誤差的方式是
（不過x不能為0），其中最小浮點數ε大約是2.2×10數量級。。以下是一個一個可以平衡捨入誤差和公式誤差，有最佳精確度的h為
上述的最小浮點數是針對雙精度（64-bit）變數，單精度變數在這類計算幾乎不太實用。其計算結果在二進制中不太可能是“整數”。雖然x是可以用浮點數表示的數字，但x+h幾乎不會也是可用浮點數表示（而且和x不同）的數字，因此x+h需調整為機器可讀的數字，因此會出現(x+h) -x不等於h的情形，因此用二個函式計算值計算微分時，二個位置的差不會是h。幾乎所有的十進制分數在二進制下都會是循環小數（都像1/3在十進制中的情形一様），例如h= 0.1在二進制下會是循環小數，是 0.000110011001100...。因此在浮點數下一個可能計算的方式是：
h:=sqrt(eps)*x; xph:=x + h; dx:=xph - x; slope:=(F(xph) - F(x))/dx;
先計算(x+h) -x的值，再用這個值作為微分算式的分母，不過若是用電腦計算，編譯器最最佳化的機能可能會認為dx和h相同，因此讓上述的方式失效。若是用C或其他類似的程式語言，可以讓xph宣告成Volatile變數，以避免此一問題。
高階方法
也有用更高階估計導數的方法，或是估計高階導數的方法。
以下就是一階導數的五點法（一維下的五點模版）
其中
微分求積
微分求積（Differential quadrature）是用函式在特定位置數值的加權和來近似導數，其名稱類似數值積分中用的求積（quadrature），也就是像梯形法或是辛普森法中用的加權和，有許多方式可找出加權的係數，在求解偏微分方程時會用到微分求積。
復變的方法
傳統用有限差分近似數值微分的方式是病態的，不過若f是全純函式，在實軸上的值都是實數，可以用複平面中靠近 x的位置來求值，此方式為數值穩定的方式，例如一階導數可以用以下的複數導數公式計算：
上述公式只在計一階導數時有效，若要拓展到任意階導數，需要用到多重複數，結果也會是多重複數的導數。
