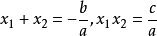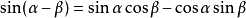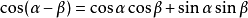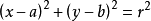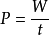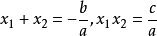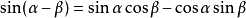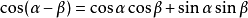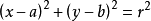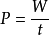基本介紹
- 中文名：公式
- 外文名：Formula
- 分類：數學
- 功能：各個量之間的一定關係
- 要求：一致性
- 套用：數學、物理學等
基本要求,相關公式,代數,幾何,相關概念,角,矩形,圓,代數公式,三角函式公式,前n項和,面積公式,國小奧數,物理公式,力學,電磁學,光學,熱學,Office,
基本要求
根據謂詞邏輯的語義推導規則，語義應該具有一致性，就是對於一個命題邏輯語句集f，若且唯若至少存在這樣一種解釋i，f的一切元素在i之下都是真的，那么，f是語義一致的。在命題邏輯語義學內，一個賦值不能同時把真和假給予某個命題原子式。在命題邏輯語義學中，在同一解釋下，一個集合不能既屬於某個謂詞的外延又不屬於該謂詞的外延。
錯誤公式特徵：
1，自稱是科學的，但含糊不清，缺乏具體的度量衡。
2，無法使用操作定義(例如，外人也可以檢驗的通用變數、屬於、或對象)
3，無法滿足簡約原則，即當眾多變數出現時，無法從最簡約的方式求得答案。
4，使用曖昧模糊的語言，大量使用技術術語來使得文章看起來像是科學的。
5，缺乏邊界條件：嚴謹的科學理論在限定範圍上定義清晰，明確指出預測現象在何時何地適用，何時何地不適用。
相關公式
代數
完全立方公式：(a+b)3=a3+3a2b+3ab2+b3;（每項係數根據楊輝三角決定）
幾何
面積計算
圓周長： 2πr（πd) 面積：
勾股定律：兩直角邊的平方和等於斜邊的平方
（首項加末項）乘項數除以2
m,n的最低公倍數為t,，最大公約數為l
那么t*l=m*n
相關概念
角
1.過兩點有且只有一條直線
2.兩點之間線段最短
3.同角或等角的補角相等
4.同角或等角的餘角相等
5.過一點有且只有一條直線和已知直線垂直
6.直線外一點與直線上各點連線的所有線段中，垂線段最短
7.平行公理 經過直線外一點，有且只有一條直線與這條直線平行
8.如果兩條直線都和第三條直線平行，這兩條直線也互相平行
9.同位角相等，兩直線平行
10.內錯角相等，兩直線平行
11.同旁內角互補，兩直線平行
12.兩直線平行，同位角相等
13.兩直線平行，內錯角相等
14.兩直線平行，同旁內角互補
15.定理 三角形兩邊的和大於第三邊
16.推論 三角形兩邊的差小於第三邊
17.三角形內角和定理三角形三個內角的和等於°
18.推論1直角三角形的兩個銳角互余
19.推論2三角形的一個外角等於和它不相鄰的兩個內角的和
20.推論3三角形的一個外角大於任何一個和它不相鄰的內角
21.全等三角形的對應邊、對應角相等
22.邊角邊公理（SAS) 有兩邊和它們的夾角對應相等的兩個三角形全等
23.角邊角公理（ASA）有兩角和它們的夾邊對應相等的兩個三角形全等
24.推論（AAS) 有兩角和其中一角的對邊對應相等的兩個三角形全等
25.邊邊邊公理（SSS) 有三邊對應相等的兩個三角形全等
26.斜邊、直角邊公理（HL) 有斜邊和一條直角邊對應相等的兩個直角三角形全等
27.定理1 在角的平分線上的點到這個角的兩邊的距離相等
28.定理2到一個角的兩邊的距離相同的點，在這個角的平分線上
29.角的平分線是到角的兩邊距離相等的所有點的集合
30.等腰三角形的性質定理 等腰三角形的兩個底角相等 （即等邊對等角）
31.推論等腰三角形頂角的平分線平分底邊並且垂直於底邊
32.等腰三角形的頂角平分線、底邊上的中線和底邊上的高互相重合
33.推論等邊三角形的各角都相等，並且每一個角都等於60 °
34.等腰三角形的判定定理 如果一個三角形有兩個角相等，那么這兩個角所對的邊也相等（等角對等邊）
35.推論1三個角都相等的三角形是等邊三角形
36.推論 2 有一個角等於°的等腰三角形是等邊三角形
37.在直角三角形中，如果一個銳角等於°那么它所對的直角邊等於斜邊的一半
38.直角三角形斜邊上的中線等於斜邊上的一半
39.定理 線段垂直平分線上的點和這條線段兩個端點的距離相等
40.逆定理 和一條線段兩個端點距離相等的點，在這條線段的垂直平分線上
41.線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合
42.定理1關於某條直線對稱的兩個圖形是全等形
43.定理2如果兩個圖形關於某直線對稱，那么對稱軸是對應點連線的垂直平分線
44.定理3兩個圖形關於某直線對稱，如果它們的對應線段或延長線相交，那么交點在對稱軸上
45.逆定理 如果兩個圖形的對應點連線被同一條直線垂直平分，那么這兩個圖形關於這條直線對稱
46.勾股定理直角三角形兩直角邊a、b的平方和、等於斜邊c的平方，即
47.勾股定理的逆定理如果三角形的三邊長a、b、c有關係
那么這個三角形是直角三角形
矩形
48定理 四邊形的內角和等於360°
49四邊形的外角和等於360°
50多邊形內角和定理n邊形的內角的和等於（n-2）×180°
51推論 任意多邊的外角和等於360°
52平行四邊形性質定理1 平行四邊形的對角相等
53平行四邊形性質定理2 平行四邊形的對邊相等
54推論 夾在兩條平行線間的平行線段相等
55平行四邊形性質定理3 平行四邊形的對角線互相平分
56平行四邊形判定定理1 兩組對角分別相等的四邊形是平行四邊形
57平行四邊形判定定理2 兩組對邊分別相等的四邊形是平行四邊形
58平行四邊形判定定理3 對角線互相平分的四邊形是平行四邊形
59平行四邊形判定定理4 一組對邊平行相等的四邊形是平行四邊形
60矩形性質定理1 矩形的四個角都是直角
61矩形性質定理2 矩形的對角線相等
62矩形判定定理1 有三個角是直角的四邊形是矩形
63矩形判定定理2 對角線相等的平行四邊形是矩形
64菱形性質定理1 菱形的四條邊都相等
65菱形性質定理2 菱形的對角線互相垂直，並且每一條對角線平分一組對角
66菱形面積=對角線乘積的一半，即S=(a×b)÷2
67菱形判定定理1 四邊都相等的四邊形是菱形
68菱形判定定理2 對角線互相垂直的平行四邊形是菱形
69正方形性質定理1 正方形的四個角都是直角，四條邊都相等
70正方形性質定理2正方形的兩條對角線相等，並且互相垂直平分，每條對角線平分一組對角
71定理1 關於中心對稱的兩個圖形是全等的
72定理2 關於中心對稱的兩個圖形，對稱點連線都經過對稱中心，並且被對稱中心平分
73逆定理 如果兩個圖形的對應點連線都經過某一點，並且被這一 點平分，那么這兩個圖形關於這一點對稱
74等腰梯形性質定理等腰梯形在同一底上的兩個角相等
75等腰梯形的兩條對角線相等
76等腰梯形判定定理在同一底上的兩個角相等的梯形是等腰梯形
77對角線相等的梯形是等腰梯形
78平行線等分線段定理如果一組平行線在一條直線上截得的線段
相等，那么在其他直線上截得的線段也相等
79 推論1 經過梯形一腰的中點與底平行的直線，必平分另一腰
80 推論2 經過三角形一邊的中點與另一邊平行的直線，必平分第 三邊
81三角形中位線定理三角形的中位線平行於第三邊，並且等於它 的一半
82梯形中位線定理梯形的中位線平行於兩底，並且等於兩底和的 一半 L=（a+b）÷2 S=L×h
83 ⑴比例的基本性質如果a:b=c:d，那么ad=bc
如果ad=bc，那么a:b=c:d wc呁/S∕
84 ⑵合比性質 如果a/b=c/d，那么（a±b)/b=(c±d)/d
85 ⑶等比性質 如果a/b=c/d=…=m/n(b+d+…+n≠0），那么
（a+c+…+m)/(b+d+…+n)=a/b
86平行線分線段成比例定理三條平行線截兩條直線，所得的對應 線段成比例
87 推論 平行於三角形一邊的直線截其他兩邊（或兩邊的延長線），所得的對應線段成比例
88 定理 如果一條直線截三角形的兩邊（或兩邊的延長線）所得的對應線段成比例，那么這條直線平行於三角形的第三邊
89 平行於三角形的一邊，並且和其他兩邊相交的直線，所截得的三角形的三邊與原三角形三邊對應成比例
90 定理 平行於三角形一邊的直線和其他兩邊（或兩邊的延長線）相交，所構成的三角形與原三角形相似
91相似三角形判定定理1 兩角對應相等，兩三角形相似（ASA）
92 直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似
93 判定定理2 兩邊對應成比例且夾角相等，兩三角形相似（SAS）
94 判定定理3 三邊對應成比例，兩三角形相似（SSS）
95 定理 如果一個直角三角形的斜邊和一條直角邊與另一個直角三 角形的斜邊和一條直角邊對應成比例，那么這兩個直角三角形相似
96 性質定理1 相似三角形對應高的比，對應中線的比與對應角平 分線的比都等於相似比
97 性質定理2 相似三角形周長的比等於相似比
98 性質定理3 相似三角形面積的比等於相似比的平方
99 任意銳角的正弦值等於它的餘角的餘弦值，任意銳角的餘弦值等 於它的餘角的正弦值
圓
101圓是定點的距離等於定長的點的集合
102圓的內部可以看作是圓心的距離小於半徑的點的集合
103圓的外部可以看作是圓心的距離大於半徑的點的集合
104同圓或等圓的半徑相等
105到定點的距離等於定長的點的軌跡，是以定點為圓心，定長為半 徑的圓
106和已知線段兩個端點的距離相等的點的軌跡，是著條線段的垂直 平分線
107到已知角的兩邊距離相等的點的軌跡，是這個角的平分線
108到兩條平行線距離相等的點的軌跡，是和這兩條平行線平行且距 離相等的一條直線
109定理 不在同一直線上的三點確定一個圓。
110垂徑定理 垂直於弦的直徑平分這條弦並且平分弦所對的兩條弧
111推論1 ①平分弦（不是直徑）的直徑垂直於弦，並且平分弦所對的兩條弧
②弦的垂直平分線經過圓心，並且平分弦所對的兩條弧
③平分弦所對的一條弧的直徑，垂直平分弦，並且平分弦所對的另一條弧
112推論2 圓的兩條平行弦所夾的弧相等
113圓是以圓心為對稱中心的中心對稱圖形
114定理 在同圓或等圓中，相等的圓心角所對的弧相等，所對的弦 相等，所對的弦的弦心距相等
115推論 在同圓或等圓中，如果兩個圓心角、兩條弧、兩條弦或兩 弦的弦心距中有一組量相等那么它們所對應的其餘各組量都相等
116定理 一條弧所對的圓周角等於它所對的圓心角的一半
117推論1 同弧或等弧所對的圓周角相等；同圓或等圓中，相等的圓周角所對的弧也相等
118推論2 半圓（或直徑）所對的圓周角是直角；90°的圓周角所 對的弦是直徑
119推論3 如果三角形一邊上的中線等於這邊的一半，那么這個三角形是直角三角形
120定理 圓的內接四邊形的對角互補，並且任何一個外角都等於它 的內對角
121①直線L和⊙O相交 d<r
②直線L和⊙O相切 d=r
③直線L和⊙O相離 d>r
122切線的判定定理 經過半徑的外端並且垂直於這條半徑的直線是圓的切線
123切線的性質定理 圓的切線垂直於經過切點的半徑
124推論1 經過圓心且垂直於切線的直線必經過切點
125推論2 經過切點且垂直於切線的直線必經過圓心
126切線長定理 從圓外一點引圓的兩條切線，它們的切線長相等， 圓心和這一點的連線平分兩條切線的夾角
127圓的外切四邊形的兩組對邊的和相等
128弦切角定理 弦切角等於它所夾的弧對的圓周角
129推論 如果兩個弦切角所夾的弧相等，那么這兩個弦切角也相等
130相交弦定理 圓內的兩條相交弦，被交點分成的兩條線段長的積 相等
131推論 如果弦與直徑垂直相交，那么弦的一半是它分直徑所成的 兩條線段的比例中項
132切割線定理 從圓外一點引圓的切線和割線，切線長是這點到割 線與圓交點的兩條線段長的比例中項
133推論 從圓外一點引圓的兩條割線，這一點到每條割線與圓的交點的兩條線段長的積相等
134如果兩個圓相切，那么切點一定在連心線上
135①兩圓外離 d>R+r ②兩圓外切 d=R+r
③兩圓相交 R-r<d<R+r(R>r)
④兩圓內切 d=R-r(R>r) ⑤兩圓內含d<R-r(R>r)
136定理 相交兩圓的連心線垂直平分兩圓的公*弦
137定理 把圓分成n(n≥3）：
⑴依次連結各分點所得的多邊形是這個圓的內接正n邊形
⑵經過各分點作圓的切線，以相鄰切線的交點為頂點的多邊形是這個圓的外切正n邊形
138定理 任何正多邊形都有一個外接圓和一個內切圓，這兩個圓是同心圓
139正n邊形的每個內角都等於(n-2)×180°/n
140定理 正n邊形的半徑和邊心距把正n邊形分成2n個全等的直角三角形
141正n邊形的面積Sn=pnrn/2（p表示正n邊形的周長）
142正三角形面積
（a表示邊長）
143如果在一個頂點周圍有k個正n邊形的角，由於這些角的和應為 360°，因此k×(n-2)180°/n=360°化為(n-2)(k-2)=4
144弧長公式=nπR/180°（n為角度制）
145扇形面積公式：S扇形=nπR2/360°=LR/2（n為角度制）
146內公切線長= d-(R-r) 外公切線長= d-(R+r)
實用工具：常用數學公式
代數公式
乘法公式與因式分解
a2-b2=(a+b)(a-b)
a3+b3=(a+b)(a2-ab+b2）
a3-b3=(a-b)(a2+ab+b2）
a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-ac-bc)
三角不等式
|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b
|a-b|≥|a|-|b| -|a|≤a≤|a|
一元二次方程
一元二次方程的解:
根與係數的關係
主詞條：韋達定理
判別式
三角函式公式
李氏三角恆等式 tanα·cotα=1
差角公式
前n項和
正弦定理
註：其中 R 表示三角形的外接圓半徑
餘弦定理
註：∠B是邊a和邊c的夾角
面積公式
圓的標準方程
註：(a,b)是圓心坐標
圓的面積公式
圓的一般方程
註：
拋物線標準方程
直稜柱側面積
斜稜柱側面積
正稜錐側面積
正稜台側面積
圓柱側面積
圓錐側面積
弧長公式l=ar a是圓心角的弧度數，r>0 扇形面積公式
斜稜柱體積 V=S'L 註：其中，S'是直截面面積， L是側棱長
柱體體積公式 V=Sh 圓柱體 :
國小奧數
和、差、倍問題公式
和差問題的公式
（和+差）÷2=大數 （和－差）÷2=小數
和倍問題的公式
和÷（倍數+1）=小數 小數×倍數=大數 （或者 和－小數=大數）
差倍問題的公式
差÷（倍數－1）=小數 小數×倍數=大數 （或 小數+差=大數）
植樹問題公式
1 非封閉線路上的植樹問題主要可分為以下三種情形：
⑴如果在非封閉線路的兩端都要植樹，那么：
株數=段數+1=全長÷株距－1
全長=株距×（株數－1）
株距=全長÷（株數－1）
⑵如果在非封閉線路的一端要植樹，另一端不要植樹，那么：
株數=段數=全長÷株距
全長=株距×株數
株距=全長÷株數
盈虧問題的公式
（盈+虧）÷兩次分配量之差=參加分配的份數
（大盈－小盈）÷兩次分配量之差=參加分配的份數
（大虧－小虧）÷兩次分配量之差=參加分配的份數
相遇問題的公式
相遇路程=速度和×相遇時間
相遇時間=相遇路程÷速度和
速度和=相遇路程÷相遇時間
追及問題公式
追及距離=速度差×追及時間
追及時間=追及距離÷速度差
速度差=追及距離÷追及時間
流水問題公式
順流速度=靜水速度+水流速度
逆流速度=靜水速度－水流速度
靜水速度=（順流速度+逆流速度）÷2
水流速度=（順流速度－逆流速度）÷2
濃度問題公式
溶質的重量+溶劑的重量=溶液的重量
溶質的重量÷溶液的重量×100%=濃度
溶液的重量×濃度=溶質的重量
溶質的重量÷濃度=溶液的重量
利潤與折扣問題公式
利潤=售出價－成本
利潤率=利潤÷成本×100%=（售出價÷成本－1）×100%
漲跌金額=本金×漲跌百分比
折扣=實際售價÷原售價×100%（折扣<1）
利息=本金×利率×時間
稅後利息=本金×利率×時間×（1－20%)
（註：1.2008年10月取消了利息稅；2.稅率要根據題目而定，不一定是20%，但如果題目沒有相關內容，則一般默認是20%）
牛吃草問題公式
"牛吃草"問題的關鍵：
⒈草場上原有的草量A
⒉草場每天生長的草量B
⒊牛每天吃的草量C
A+B*天數=牛的數量*吃的天數*C
物理公式
力學
速度v(m/s)
; s：位移，t：時間
重力G(N) G=mg; m：質量 ; g：9.8N/kg或者10N/kg
密度ρ(kg/m3) ρ= m/V m：質量;V：體積
合力F合(N) 方向相同：F合=F1+F2
方向相反：F合=F1-F2 方向相反時，F1>F2
浮力F浮(N) F浮=G物-G視 ;G視：物體在液體的視重（測量值）
浮力F浮(N) F浮=G物; 此公式只適用物體漂浮或懸浮
浮力F浮(N) F浮=G排=m排g=ρ液gV排；G排：排開液體的重力，m排：排開液體的質量，ρ液：液體的密度，V排：排開液體的體積(即浸入液體中的體積)
槓桿的平衡條件 F1L1= F2L2；F1：動力， L1：動力臂，F2：阻力，L2：阻力臂
定滑輪 F=G物,S=h, F：繩子自由端受到的拉力，G物：物體的重力，S：繩子自由端移動的距離，h：物體升高的距離
動滑輪 F= (G物+G輪)/2，S=2 h，G物：物體的重力, G輪：動滑輪的重力
滑輪組 F= (G物+G輪)/n，S=nh，n：承擔物重的段數
機械功W(J) W=Fs F：力 S：在力的方向上移動的距離
有用功:W有,總功:W總, W有=G物h，W總=Fs，適用滑輪組豎直放置時機械效率 η=W有/W總×100%
功 W = Fs = Pt ；1J = 1N·m = 1W·s
功率 P = W / t = Fv(勻速直線) 1kW = 103 W，1MW = 103kW
有用功 W有用 = Gh= W總 – W額 =ηW總
額外功 W額 = W總 – W有 = G動 h(忽略輪軸間摩擦)= f L(斜面)
總功 W總= W有用+ W額 = Fs= W有用/η
機械效率 η=G /(nF)= G物 /(G物 + G動) 定義式適用於動滑輪、滑輪組
功率P(w) P= W/t; W：功 ;t：時間
壓強p(Pa) P= F/S F：壓力/S：受力面積
液體壓強p(Pa) P=ρgh ρ：液體的密度h：深度(從液面到所求點的豎直距離)
熱量Q(J) Q=cm△t c：物質的比熱容 m：質量,△t：溫度的變化值
燃料燃燒放出的熱量Q(J) Q=mq ;m：質量,q：熱值
功 W 焦耳(焦) J W=Fs
功率 P 瓦特(瓦) w
電流 I 安培(安) A I=U/R
電壓 U 伏特(伏) V U=IR
電阻 R 歐姆(歐)
電功 W 焦耳(焦) J W=UIt
電功率 P 瓦特(瓦) W
熱量 Q 焦耳(焦) J Q=cm(t-t°)
比熱 c 焦/(千克°C) J/(kg·°C)
真空中光速 3×108米/秒
g=9.8kg·m/s2
15°C空氣中聲速 340米/秒
電磁學
串聯電路
電流I(A) I=I1=I2=…… 電流處處相等
電壓U(V) U=U1+U2+…… 串聯電路起分壓作用
電阻R(Ω) R=R1+R2+……
並聯電路
電流I(A) I=I1+I2+…… 幹路電流等於各支路電流之和(分流)
電壓U(V) U=U1=U2=……
電阻1/R(Ω) =1/R1+1/R2
部分電路歐姆定律
閉合電路歐姆定律
電路中的電流與電壓成正比，與電阻成反比
電流定義式 I= Q/t：電荷量(庫侖)t：時間(S)
電功W(J) W=UIt=Pt；U：電壓 I：電流t：時間 P：電功率
電功率
U:電壓； I：電流R：電阻
光學
電磁波波速與波長、頻率的關係 c=λf
c：波速(電磁波的波速是不變的，等於3×108m/s) λ：波長 f：頻率
熱學
溫度 t 攝氏度 °C
速度 v 米/秒 m/s v=s/t
密度 ρ 千克每立方米kg/m3
安全電壓 不高於36伏
Office
Microsoft Word和Office網站提供了多種常用的公式供用戶直接插入到Word文檔中，以Word2010軟體為例介紹方法：
第1步，打開Word2010文檔視窗，切換到“插入”功能區。
第2步，在“符號”分組中單擊“公式”下拉三角按鈕，在打開的內置公式列表中選擇需要的公式（如“二次公式”）即可。
在當前計算機處於聯網狀態下，如果在Word2010提供的內置公式中找不到用戶需要的公式，則可以在公式列表中指向“Office中的其他公式”選項，並在打開的來自Office網站的更多公式列表中選擇所需的公式。
