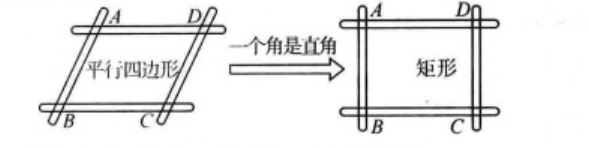
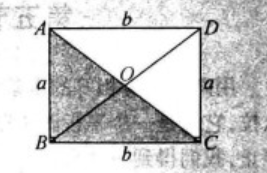
矩形性質定理是數學中一個幾何概念，有一個角是直角的平行四邊形是矩形。矩形對邊平行且相等，四個角都是直角，矩形對角線互相平分且相等。中國古算書中，將矩形田稱為直田，也稱矩形圖形為直田。
基本介紹
- 中文名：矩形性質定理
- 別稱：矩形定理
- 套用學科：數學
- 適用領域範圍：數理科學
- 矩形定義：一個角是直角的平行四邊形
- 性質：對角線互相平分且相等
矩形,性質定理,判定定理,套用,
矩形
長方形也稱矩形，是特殊的平行四邊形之一。即有一個角是直角的平行四邊形稱為長方形。中國古算書中，將矩形田稱為直田，也稱矩形圖形為直田。
用兩組對應相等的木條可以做一個活動的平行四邊形木框。輕輕拉動一個點，不管怎么拉，它還是一個平行四邊形。再次演示平行四邊形的移動過程，當移動到一個角是直角時停止，我們得到一個長方形。
定義：有一個角是直角的平行四邊形叫做矩形（長方形）。
周長和面積公式：
如下圖，矩形ABCD的周長=2（a+b）；
矩形ABCD的面積S=ab。（當a=b時，可以得到正方形的相應公式）
性質定理
在國小，矩形是我們最熟悉的圖形之一。很自然地，我們可以得出矩形的以下性質：
矩形的性質定理1
1、矩形的對邊平行且相等。
2、矩形的四個角都是直角。
矩形的性質定理2
1、矩形的對角線相等。
平行四邊形ABCD：AC=BD
2、矩形的對角線相互平分。
平行四邊形ABCD是矩形：OA=OC，OB=OD
矩形的對角線相等，我們可以通過勾股定理證明。
證明：∵△ABC中，∠ABC =90°，
∴AC2=a2+b2
∵△DCB中，∠BCD =90，
∴BD2= a2+ b2
∴AC2=BD2
∴AC=BD
判定定理
要畫矩形，最簡單的辦法，就是用直角三角板依次畫三個直角，所得的四邊形就是矩形。
判定定理1：有三個角是直角的四邊形是矩形。
判定定理2：對角線相等的平行四邊形是矩形。
套用
1、矩形容器
矩形截面容器主要用於石化、造紙、醫藥及環保等工業，在人們日常生活中也經常見到這種容器。在結構尺寸和壁厚相同情況下，矩形截面容器與圓柱殼容器相比，承載能力要差得多。
矩形容器結構形式有帶加強圈和無加強圈結構形式，在這兩種容器中，還有帶孔和不帶孔之分。對於疲勞載荷作用的矩形容器如消毒器，容器縱向拐角處應帶有大於壁厚3倍的內半徑的圓弧；對於帶門的容器，要特別注意開門和容器邊角的變形和開門密封墊片的選擇。
矩形容器設計主要是計算殼體最危險部位的薄膜應力和彎曲應力，最大應力是薄膜應力與彎曲應力的總和。
2、矩形管
