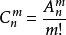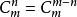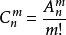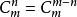組合數公式是指從n個不同元素中，任取m(m≤n)個元素並成一組，叫做從n個不同元素中取出m個元素的一個組合；從n個不同元素中取出m(m≤n)個元素的所有組合的個數，叫做n個不同元素中取出m個元素的組合數。用符號c(m,n) 表示。
基本介紹
- 中文名：組合數公式
- 外文名：Combination Number Formula
- 公式寫法：c(m,n)=p(m,n)/n!
- 遞推公式：c(m,n)=c(m-1,n-1)+c(m-1,n)
- 套用領域：數學等
公式,性質,遞推公式,算法舉例,
公式
有時候也表示成：
組合公式的推導是由排列公式去掉重複的部分而來的，排列公式是建立一個模型，從n個不相同元素中取出m個排成一列（有序），第一個位置可以有n個選擇，第二個位置可以有n-1個選擇（已經有1個放在前一個位置），則同理可知第三個位置可以有n-2個選擇，以此類推第m個位置可以有n-m+1個選擇，則排列數為
，而組合公式對應另一個模型,取出m個成為一組（無序）,由於m個元素組成的一組可以有m!種不同的排列（全排列
）,組合的總數就是
性質
遞推公式
c(m,n)=c(m-1,n-1)+c(m-1,n)
等式左邊表示從m個元素中選取n個元素，而等式右邊表示這一個過程的另一種實現方法：任意選擇m中的某個備選元素為特殊元素，從m中選n個元素可以由此特殊元素的被包含與否分成兩類情況，即n個被選擇元素包含了特殊元素和n個被選擇元素不包含該特殊元素。前者相當於從m-1個元素中選出n-1個元素的組合，即c(m-1,n-1)；後者相當於從m-1個元素中選出n個元素的組合，即c(m-1,n)。
c(n,0)+c(n,1)+c(n,2)+……+c(n,n)=2的n次方
相關運用：（a+b）的n次方的二項式定理的係數，即為此數列；任何集合的子集個數也為用為此數列，而得出為2的n次方個。
算法舉例
1、設15000件產品中有1000件次品，從中拿出150件，求得到次品數的期望和方差？
2、設某射手對同一目標射擊，直到射中R次為止，記X為使用的射擊次數，已知命中率為P，求E（X）、D（X）。
這兩題都要用到一些技巧。我先列出幾個重要公式，證明過程中提供變換技巧，然後把這兩個題目作為例題。
先定義一個符號，用S（K=1，N）F（K）表示函式F（K）從K=1到K=N求和。
公式1：
C（M-1，N-1）+C（M-1，N）=C（M，N）
公式1 證明：
方法1、可直接利用組合數的公式證明。
方法2、（更重要的思路）。
從M個元素中任意指定一個元素。則選出N個的方法中，包含這一個元素的有C（M-1，N-1）種組合，不包含這一個元素的有C（M-1，N）種組合。
因此，C（M-1，N-1）+C（M-1，N）=C（M，N）
公式2：
S（K=N，M）C（K-1，N-1）=C（M，N） （M》=N）
證明：C（M，N）是從M個物品中任選N個的方法。
從M個物品中任意指定M-N個，並按次序編號為第1到第M-N號，而其餘的還有N個。
則選出N個的方法可分類為：
包含1號的有C（M-1，N-1）種；
不包含1號，但包含2號的有C（M-2，N-1）種；
。。。。。。
不包含1到M-K號，但包含M-K+1號的有C（K-1，N-1）種
。。。。。。
不包含1到M-N-1號，但包含M-N號的有C（N，N-1）種不包含1到M-N號的有C（N，N）種，而C（N，N）=C（N-1，N-1）
由於兩種思路都是從M個物品中任選N個的方法，因此
S（K=N，M）C（K-1，N-1）=C（M，N）
公式3：
S（K=0，N）C（P，K）*C（Q，N-K）=C（P+Q，N） （P，Q）=N）
證明：一批產品包含P件正品和Q件次品，則從這批產品中任選N件的選法為C（P+Q，N）。而公式裡面的K表示選法中正品數量，
C（P，K）*C（Q，N-K）表示N件產品中有K件正品，N-K件次品的選法。K從0到N變化時，就包含了所有不同正品、次品數的組合。
因此，S（K=0，N）C（P，K）*C（Q，N-K）=C（P+Q，N）
公式4（一種變換技巧）：
S（K=0，N）K*C（M，K）=S（K=0，N-1）M*C（M-1，K）
證明：
S（K=0，N）K*C（M，K）
=S（K=1，N）K*C（M，K）
=S（K=1，N）K*M！/K！/（M-K）！
=S（K=1，N）M*（M-1）！/（K-1）！/（M-K）！
=S（K=1，N）M*C（M-1，K-1）
=S（K=0，N-1）M*C（M-1，K）
公式5（公式4的同種）
S（K=0，N）K*（K-1）*C（M，K）
=S（K=0，N-2）M*（M-1）*C（M-2，K）
證明：（類似上式）
S（K=0，N）K*（K-1）*C（M，K）
=S（K=2，N）K*（K-1）*M！/K！/（M-K）！
=S（K=2，N）M*（M-1）*（M-2）！/（K-2）！/（M-K）！
=S（K=2，N）M*（M-1）*C（M-2，K-2）
=S（K=0，N-2）M*（M-1）*C（M-2，K）
公式4用於求數學期望，公式4、公式5結合起來可用於求方差。
例1、設15000件產品中有1000件次品，從中拿出150件，求得到次品數的期望和方差？
解：（本題利用公式3、4、5）
有K件次品的機率為：
P（K）=C（1000，K）*C（14000，150-K）/C（15000，150）
E（X）
=S（K=0，150）K*C（1000，K）*C（14000，150-K）/C（15000，150）
=S（K=0，149）1000*C（999，K）*（14000，149-K）/C（15000，150）
=1000*C（14999，149）/C（15000，150）
=10
D（X）
=S（K=0，150）（K-10）*（K-10）*C（1000，K）*C（14000，150-K）/C（15000，150）
=S（K=0，150）（K*K-K-19*K+100）*C（1000，K）*C（14000，150-K）/C（15000，150）
=S（K=0，150）K*（K-1）*C（1000，K）*C（14000，150-K）/C（15000，150）
-19*S（K=0，150）K*C（1000，K）*C（14000，150-K）/C（15000，150）
+100*S（K=0，150）C（1000，K）*C（14000，150-K）/C（15000，150）
=S（K=0，148）1000*999*C（998，K）*C（14000，148-K）/C（15000，150）
-19*S（K=0，149）*1000*C（999，K）*C（14000，149-K）/C（15000，150）
+100*S（K=0，150）C（1000，K）*C（14000，150-K）/C（15000，150）
=1000*999*C（14998，148）/C（15000，150）
-19*1000*C（14999，149）/C（15000，150）+100
=138600/14999
=9.240616041
此題推廣形式為：
設M件產品中有P件次品，從中拿出N件（N《=P），求得到次品數的期望和方差？
E（X）=P*N/M
D（X）=P*（P-1）*C（M-2，N-2）/C（M，N）
+（1-2*P*N/M）*P*C（M-2，N-2）/C（M，N）+（P*N/M）^2
例2、設某射手對同一目標射擊，直到射中R次為止，記X為使用的射擊次數，已知命中率為P，求E（X）、D（X）。
解：射中R次，使用的射擊次數為K次(K>=R)，則前K-1次射中R-1次，第K次射中了，機率為：
P（K）=C（K-1，R-1）*P^R*(1-P)^(K-R)
(以下暫時用W表示無窮大）
射中R次，使用的射擊次數可為R次、R+1次...W次
因此S（K=R，W）P（K）=1 （這是機率的特點）
即：S（K=R，W）C（K-1，R-1）*P^R*(1-P)^(K-R)=1
以上證明的式子是另一個公式，即無論P，R是什麼數都成立，以下將套用這一公式。
E（X）
=S（K=R，W）K*C（K-1，R-1）*P^R*(1-P)^(K-R)
=S（K=R，W）K*（K-1）！/（R-1）！/（K-R）！*P^R*(1-P)^(K-R)
=S（K=R，W）R*K！/R！/（K-R）！*P^R*(1-P)^(K-R)
=S（K=R，W）R*C（K，R）*P^R*(1-P)^(K-R)
=R/P*S（K=R，W）C（K，R）*P^（R+1）*(1-P)^(K-R)
令K1=K+1，R1=R+1，則
E（X）=R/P*S（K1=R1，W）C（K1-1，R1-1）*P^R1*(1-P)^(K1-R1)
利用以上公式得
E（X）=P/R
D（X）
=S（K=R，W）（K-R/P）^2*C（K-1，R-1）*P^R*(1-P)^(K-R)
=S（K=R，W）（K*K-2*K*R/P+R*R/P/P）*C（K-1，R-1）*P^R*(1-P)^(K-R)
=S（K=R，W）[K*（K+1）-（K+2*K*R/P）+R*R/P/P]*C（K-1，R-1）*P^R*(1-P)^(K-R)
=S（K=R，W）[K*（K+1）*C（K-1，R-1）*P^R*(1-P)^(K-R)
-S（K=R，W）（K+2*K*R/P）*C（K-1，R-1）*P^R*(1-P)^(K-R)
+S（K=R，W）R*R/P/P*C（K-1，R-1）*P^R*(1-P)^(K-R)
=（推導過程同求E（X），略）
=R（R+1）/P/P-（2*R+P）*R/P/P+R*R/P/P
=（1-P）*R/P/P
