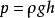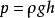在液體容器底、內壁、內部中，由液體本身的重力而形成的壓強稱為液體壓強，簡稱液壓。
帕斯卡“桶裂”實驗可以很好地證明液體壓強與液體的深度有關，因為液體的壓強等於密度、深度和重力常數之積。在這個實驗中，水的密度不變，但深度一再增加，則下部的壓強越來越大，其液壓終於超過木桶能夠承受的上限，木桶隨之裂開。
基本介紹
帕斯卡,帕斯卡定律,公式,影響因素,壓強測量,裂桶實驗,
帕斯卡
帕斯卡定律
在幾百年前，帕斯卡注意到一些生活現象，如沒有灌水的水龍帶是扁的．水龍帶接到自來水龍頭上，灌進水，就變成圓柱形了．如果水龍帶上有幾個眼，就會有水從小眼裡噴出來，噴射的方向是向四面八方的．水是往前流的，為什麼能把水龍帶撐圓？
通過觀察，帕斯卡設計了“帕斯卡球”實驗，帕斯卡球是一個壁上有許多小孔的空心球，球上連線一個圓筒，筒里有可以移動的活塞．把水灌進球和筒里，向里壓活塞，水便從各個小孔里噴射出來了，成了一支“多孔水槍”
帕斯卡球的實驗證明，液體能夠把它所受到的壓強向各個方向傳遞．通過觀察發現每個孔噴出去水的距離差不多，這說明，每個孔所受到的壓強都相同。
帕斯卡通過“帕斯卡球”實驗，得出著名的帕斯卡定律：加在密閉液體任一部分的壓強，必然按其原來的大小，由液體向各個方向傳遞。這就是歷史上有名的帕斯卡桶裂實驗。 一個容器里的液體，對容器底部(或側壁)產生的壓力遠大於液體自身的重量，這對許多人來說是不可思議的。我們知道，物體受到力的作用產生壓力，而只要某物體對另一物體表面有壓力，就存在壓強，同理，水由於受到重力作用對容器底部有壓力，因此水對容器底部存在壓強。液體具有流動性，對容器壁有壓力，因此液體對容器壁也存在壓強。
在國中階段，液體壓強原理可表述為：“液體內部向各個方向都有壓強，壓強隨液體深度的增加而增大，同種液體在同一深度的各處，各個方向的壓強大小相等；不同的液體，在同一深度產生的壓強大小與液體的密度有關，密度越大，液體的壓強越大。”
特點：加在封閉液體上的壓強能夠大小不變地被液體向各個方向傳遞。
同種液體在同一深度液體向各個方向的壓強都相等。
公式
液體壓強的公式為：
固體壓強也可用P=ρgh計算，但只參考密度均勻的幾何直柱體，其上下底面積相等。
其表達式可以轉化為：
深度是指點到自由液面的距離，液體的壓強與深度和液體的密度有關，與液體的質量無關.
液體壓強產生原因：受重力、且有流動性。
影響因素
1.由於液體具有流動性，它所產生的壓強具有如下幾個特點：
(1)液體除了對容器底部產生壓強外，還對“限制”它流動的側壁產生壓強。固體則只對其支承面產生壓強，方向總是與支承面垂直。
(2)在液體內部向各個方向都有壓強，在同一深度向各個方向的壓強都相等。同種液體，深度越深，壓強越大。
(3)計算液體壓強的公式是p=ρgh。可見，液體壓強的大小隻取決於液體的種類(即密度ρ)和深度h，而和液體的質量、體積沒有直接的關係。
(4)密閉容器內的液體能把它受到的壓強按原來的大小向各個方向傳遞。與重力無關。
2.容器底部受到液體的壓力跟液體的重力不一定相等。容器底部受到液體的壓力F=pS=ρghS,其中“h”底面積為S，“hS”為高度為h的液柱的體積，“ρghS”是這一液柱的重力。因為液體有可能傾斜放置。 所以，容器底部受到的壓力其大小可能等於，也可能大於或小於液體本身的重力。若杯為上小下大，則液體對杯底的壓力大於液體本身的重力。若杯為上大下小，則液體對杯底的壓力小於液體本身的重力。若杯上下部分大小相等，則液體對杯底的壓力等於液體本身的重力。
在U型玻璃管內盛了有色的水，玻璃管一端用橡皮管連線一個開有小孔的金屬盒，金屬盒上蒙有一層橡皮膜。未對橡皮膜加壓時，U型兩管中的水面在同一高度上，用力壓橡皮膜時，跟盒相連的管中壓強變大，水面就下降，另一管中水面上升。加在橡皮模上的壓強越大，兩管中水面的高度差就越大。
把壓強計的金屬盒放入水中時，根據兩管中水面的高度差就可以反應橡皮膜受到水的壓強的大小了。
壓強測量
液體壓強的測量儀器叫“U形管壓強計”，利用液體壓強公式p=ρhg，h為液體的深度，計算液面差產生的壓強就等於液體內部壓強。
公式：F1/S1=F2/S2
非直立柱體時液體對容器底部的壓強,可用P=ρgh計算，不能用P=F/S計算；非直立柱體時液體對容器底部的壓力，可用F=PS=ρghS計算。因為同學對這個問題疑問較多，對P=F/S和P=ρgh兩個公式簡單說明如下：由P=F/S是可以推導出液體壓強公式 P=ρgh，但這是在液體容器為規則均勻的柱體容器的前提下推導出來的，所以公式P=F/S的使用條件僅適用於這種柱體容器（這一點與固體不同，固體間的壓強總是可以用P=F/S來計算）。但 P=ρgh這個公式根據液體本身的特性（易流性，連通器原理、帕斯卡定律等）可以推廣到任意形狀的容器，只要是連通的密度均勻的液體都可以用。其實液體內部壓強公式的推導完全可以不用公式P=F/S來推導，而是用更加普遍、更加一般的方法——質量力的勢函式的積分來推導，只是這已超出中學的教學大綱了。由於液體的易流性和不可拉性，靜止的液體內部沒有拉應力和切應力，只能有壓應力（即壓強），在靜止的液體內部任意取出微小一個六面體，這個六面體在六個面的支持力和本身的重力共同作用下處於平衡狀態，構想這個六面體無限縮小時，其重力可以忽略不計，就得出作用在同一點上的各個方向的壓強相等，即壓強僅僅與位置坐標有關，而與方位無關。即 P=f(x,y,z)。再構想坐標x-O-y處在水平面上，z為豎直向下的坐標。液體的壓強是由液體的質量力引起的，當液體對地球來說是靜止時，就是由重力引起的，液體質量m=1的液體單位質量力在各坐標的分量為X=0、Y=0、Z=g，液體內部的壓強與質量力的微分關係為dP=ρ(XdxYdy+Zdz)=ρ(0*dx+0*dy+gdz)=ρgdz (從本方程看出在同一水平面上沒有壓強差，水平面是等壓面，即前後左右壓強都相等，壓強僅在重力方向上有變化）。從水面z=0到水深z=h積分上式得 P=ρgh。
影響液體壓強的因素：深度，液體的密度（與容器的形狀，液體的質量體積無關）
裂桶實驗
帕斯卡在1648年表演了一個著名的實驗：他用一個密閉的裝滿水的桶，在桶蓋上插入一根細長的管子，從樓房的陽台上向細管子裡灌水。結果只倒了幾杯水，桶就裂了，桶里的水就從裂縫中流了出來。原來由於細管子的容積較小，幾杯水灌進去，其深度(h)很大。壓強也隨之變大，最終導致水桶破裂。
