基本介紹
- 中文名:梯形中位線定理
- 外文名:Median line theorem of trapezium
- 表達式:S=(a+b)÷2 S梯=2Lh÷2=Lh
- 套用學科:數學
- 適用領域範圍:幾何學
- 適用領域範圍:數學、物理、建築等
- 梯形的中位線:連線梯形兩腰中點的線段
定理定義
驗證推導
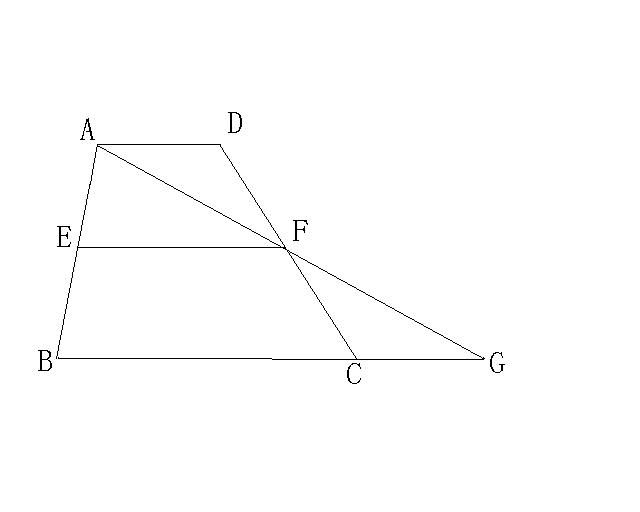 梯形中位線定理證明
梯形中位線定理證明特例做法


 梯形中位線定理證明
梯形中位線定理證明
梯形中位線定理是幾何學的一個定理,是指連線梯形兩腰中點的線段叫做梯形的中位線,梯形的中位線平行於兩底,並且等於兩底和的一半 。...
連線梯形兩腰中點的線段叫做梯形的中位線,梯形的中位線平行於兩底,並且等於兩底和的一半。...
中位線是在三角形或梯形中一條特殊的線段,與其所在的三角形或梯形有著特殊的關係。連線三角形的兩邊中點的線段叫做三角形的中位線。三角形有三條中位線,首尾相...
中位線是一個數學術語,至平面幾何內的三角形任意兩邊中點的連線或梯形兩腰中點的連線。連線三角形兩邊中點的線段叫做三角形的中位線,三角形的中位線平行於第三邊...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...梯形中位線定理WWolstenholme定理無限猴子定理威爾遜定理魏爾施特拉斯逼近定理...
81三角形中位線定理三角形的中位線平行於第三邊,並且等於它的一半82 梯形中位線定理 梯形的中位線平行於兩底,並且等於兩底和的一半 l=(a+b)÷2 s=l×h...
81三角形中位線定理三角形的中位線平行於第三邊,並且等於它 的一半 82梯形中位線定理梯形的中位線平行於兩底,並且等於兩底和的 一半L=(a+b)÷2 S=L×h...
81三角形中位線定理三角形的中位線平行於第三邊,並且等於它的一半82 梯形中位線定理 梯形的中位線平行於兩底,並且等於兩底和的一半 l=(a+b)÷2 s=l×h...
81、三角形中位線定理:三角形的中位線平行於第三邊,並且等於它的一半82、梯形中位線定理:梯形的中位線平行於兩底,並且等於兩底和的...
39三角形中位線定理的運用 40巧用梯形的中位線定理證題 41四邊形中的等邊三角形 42構造等腰三角形解題 43用同一法巧證幾何題 44設而不求巧解幾何題 相似形...
10.梯形及其中位線定理 11.數的開方 12.無理數的整數、小數部分的套用 13.二次根式的概念與性質 14.二次根式的化簡 15.比例線段 16.相似三角形(一) 相似三...
126 矩形的判定定理 127 菱形的性質 128 菱形的面積公式 129 菱形的判定定理 130 正方形的判定 131 等腰梯形的性質與判定 132 梯形中位線定理 133 ...
81三角形中位線定理三角形的中位線平行於第三邊,並且等於它 的一半82梯形中位線定理梯形的中位線平行於兩底,並且等於兩底和的 一半 L=(a+b)÷2 S=L×h...
