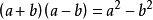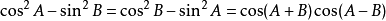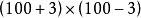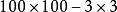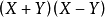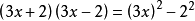平方差公式（formula for the difference of square）是指兩個數的和與這兩個數差的積，等於這兩個數的平方差，表達式是(a+b)(a-b)=a2-b2。
基本介紹
- 中文名：平方差公式
- 外文名：formula for the difference of square
- 表達式：(a+b)(a-b)=a2-b2
- 套用學科：數學
- 適用領域範圍：三角
- 適用領域範圍：代數
- 包含：代數平方差公式和三角平方差公式
代數平方差公式,定義,說明,變化形式,常見錯誤,注意事項,三角平方差公式,例題,
代數平方差公式
定義
兩個數的和與這兩個數的差的積等於這兩個數的平方差，用字母表示為
。運用
可用於某些分母含有根號的分式：請看下列
[解方程]
[解題過程]
因為1991可以分成996和995
所以如果
，
，解得x=996，y=995
如果x+y=181，x-y=11，x=96，y=85同時也可以是負數
所以解有x=996，y=995，或x=996，y=-995，或x=-996，y=995或x=-996，y=-995
或x=96，y=85，或x=96，y=-85或x=-96，y=85或x=-96，y=-85
有時應注意加減的過程。
說明
當除式是兩個數之和以及這兩個數之差相乘時，積是二項式。這是因為具備這樣特點的兩個二項式相乘，積的四項中，會出現互為相反數的兩項，合併這兩項的結果為零，於是就剩下兩項了。而它們的積等於乘式中這兩個數的平方差，即
，兩數的和與這兩數的差的積，就是它們的平方差，請看下列
[正推導平方差公式]
[逆推導平方差公式]
變化形式
公式
有4種形式變化：
位置變化
符號變化
係數變化
指數變化
常見錯誤
平方差公式中常見錯誤：（注意）
①學生難於跳出原有的定式思維，如典型錯誤；（錯因：在公式的基礎上類推，隨意“創造”）
②混淆公式；
③運算結果中符號錯誤；
④變式套用難以掌握。
注意事項
- 公式的左邊是個兩項式的積，有一項是完全相同的。
- 右邊的結果是乘式中兩項的平方差，相同項的平方減去相反項的平方。
- 公式中的a.b 可以是具體的數，也可以是單項式或多項式。
三角平方差公式
- 三角函式公式中，有一組公式被稱為三角平方差公式：
這組公式是化積公式的一種，由於酷似平方差公式而得名，主要用於解三角形。
例題
一，利用公式計算
(1)
解：原式 =
=
=
=
=
(2)
解：原式 =
=
(3)
解：原式=
(4)
(5)
(6)
解（1）中可以把3x看作a，2看作b． 即：
【即為
】同樣的方法可以完成（2）、（3）。如果形式上不符合公式特徵，可以做一些簡單的轉化工作，使它符合平方差公式的特徵．比如（2）應先作如下轉化：
． 如果轉化後還不能符合公式特徵，則應考慮多項式的乘法法則。
