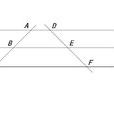
平行線分線段成比例定理指的是兩條直線被一組平行線(不少於3條)所截,截得的對應線段的長度成比例。推論:平行於三角形一邊的直線,截其他兩邊(或兩邊延長線)所得的對應線段成比例。
基本介紹
- 中文名:平行線分線段成比例定理
- 外文名:Parallel line segment proportion theorem
- 套用學科:數學
- 適用領域範圍:平面幾何、立體幾何
- 適用領域範圍:相似三角形
- 內容:三條平行線截兩條直線線段成比例
- 證明:用三角形面積可以證明
- 等級:國中
簡介

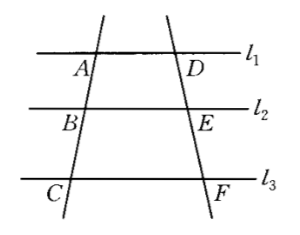 圖1
圖1定理證明
根據平行線的性質可得 S△ABE=S△DBE, S△BCE=S△BEF,
∴S△ABE/S△CBE=S△DBE/S△BFE
根據同底等高三角形面積比等於底的比可得:AB/BC=DE/EF。
由更比性質、等比性質得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF。
定理推論
三條平行線截兩條直線,所得對應線段成比例。
推廣:過一點的一線束被平行線截得的對應線段成比例。
定理推論:
①平行於三角形一邊的直線截其它兩邊(或兩邊的延長線)所得對應線段成比例。
②平行於三角形一邊,並且和其他兩邊相交的直線,所截得的三角形的三邊與原三角形的三邊對應成比例。