布利安桑定理

布利安桑（Brainchon）定理是一個射影幾何中的著名定理，其定理內容為：六條邊和一條圓錐曲線相切的六邊形的三條對角線共點，此點被稱為該六邊形的布列安桑點。

基本介紹

• 中文名：布利安桑定理
• 外文名：Brainchon
• 提出者：Brainchon
• 提出時間：1806
• 套用學科：數學
• 適用領域範圍：平面幾何

定理定義

布利安桑定理敘述如下：如果六邊形的邊交替地通過兩個定點P和Q，則連線六邊形的相對的頂點的三條對角線是共點的。

布列安桑（Brainchon）定理是一個射影幾何中的著名定理，它斷言六條邊和一條圓錐曲線相切的六邊形的三條對角線共點，此點稱為該六邊形的布列安桑點（見下圖）：

[注1] 此處的對角線指主對角線，若六邊形的六個頂點記作 A1, A2, A3, A4, A5, A6，則三條（主）對角線為 A1A4, A2A5, A3A6.

定理證明

證明一

（利用根軸）（定理中圓錐曲線為圓的情況）

證明一

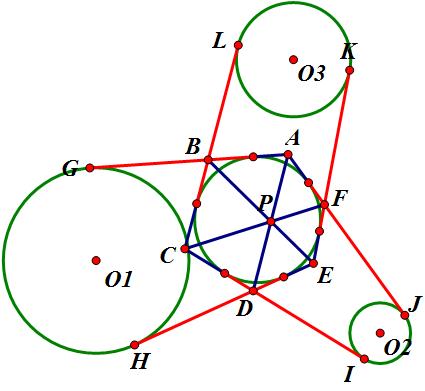
已知：如圖所示，正六邊形ABCDEF外切於一圓。

求證：AD，BE，CF共點。

證明：如圖所示，從外切六邊形的各個切點如圖方向延長，使圖中所有紅色的線段相等。（即若設AB、BC、CD、DE、EF、FA分別切圓於G'、L'、I'、H'、K'、J'，則分別延長AB、CB、CD、ED、EF、AF到G、H、I、J、K、L，而且滿足GG'=HH'=II'=JJ'=KK'=LL'）分別過G、H為切點作圓O1，I、J為切點作圓O2，K、L為切點作圓O3

由切線長定理易推出GB=BL，HE=KE，所以BE為圓O1和圓O3的根軸，

同理可證CF為圓O2和圓O3的根軸，AD為圓O1和圓O2的根軸，

由根心定理知，三個不在一條直線的三個圓的三條根軸必交於一點，所以AD，BE，CF共點，

得證

證明二

（利用牛頓定理3）（定理中圓錐曲線為圓的情況）

如右圖所示。

--------------------（以下為右圖中的內容）---------------------------------------

已知：如圖所示，六邊形ABCDEF外切於一圓。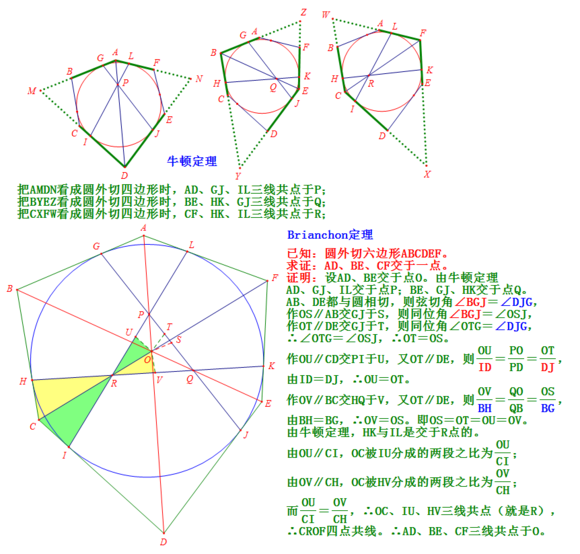

證明二

求證：AD、BE、CF交於一點。

證明：設AD、BE交於點O。AB、BC、CD、DE、EF、FA分別切圓於G、H、I、J、K、L。

由牛頓定理3知AD、GJ、IL交於點P；BE、GJ、HK交於點Q，CF、HK、IL交於點R。

由弦切角定理易得∠BGJ=∠DJG，

作OS//AB交GJ於S，OT//DE交GJ於T，則∠OTS=180°-∠DJG=180°-∠BGJ=∠OST，所以OT=OS，

作OU//CD交PI於U，又因為OT//DE，則OU/ID=PO/PD=OT/DJ（平行線分線段成比例定理），

由切線長定理知ID=DJ，所以OU=OT，

作OV//BC交HQ於V，同理可證OV=OS，

所以OU=OT=OS=OV，

因為OU//CI，所以OC被IU分成的兩段之比為OU/CI（平行線分線段成比例定理），

因為OV//CH，所以OC被HV分成的兩段之比為OV/CH（平行線分線段成比例定理），

又因為OU=OV（已證），CI=CH（切線長定理），

所以OU/CI=OV/CH，即IU、OC的交點與HV、OC的交點重合，所以IU、OC、HV共點，

又因為CF、HK、IL共點（已證），所以C、O、F共線，即AD、BE、CF共點，

得證。

--------------------（以上為右圖中的內容）---------------------------------------

定理推廣

此定理是帕斯卡定理的對偶形式。用其證明牛頓定理甚易。

布列安桑定理的逆定理亦同樣成立，即如果一個六邊形的三條對角線共點，則它的六條邊和一條圓錐曲線相切。

發展簡史

布列安桑定理由法國數學家 Charles Julien Brianchon (1783–1864) 發現， 按照法語發音，Brianchon 應該譯為“布里昂雄”，現在的數學名詞譯者多不懂法語，誤按英語發音譯為“布列安桑”，此名詞已廣為人知，故從之。

布列安桑定理是射影幾何中的另一個著名定理——帕斯卡（Pascal）定理的對偶定理。