基本介紹
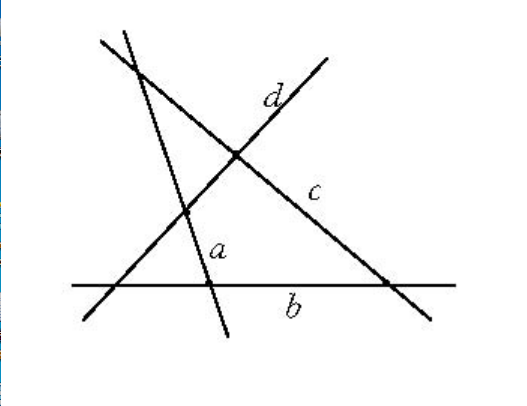
由四條直線(其中無三者共點)a,b,c,d及它們順次兩兩交點(a,b),(b,c),(c,d)、(d,a)所組成的平面形叫做簡單四線形。a,b,c,d叫做邊,(a,b),(b,c),(c,d),(d,a)叫做頂點,不順次兩邊的交點(a,c),(b,d)叫做對邊點(圖1)。
 圖1
圖1簡單四點形 由四個點(其中無三者共線)A,B,C,D及它們順次兩兩的連線AB,BC,CD,DA所組成的平面形叫做簡單四點形。A,B,C,D叫做頂點。AB,BC,CD,DA叫做邊,不順次的頂點的連線AC,BD做對頂線(圖2)。
注意:簡單四點形的構成與頂點的順序有關,如圖2表示四點形ABCD,它與四點形ACBD,BDAC等不同,同樣,簡單四線形的構成與邊的順序有關。
 圖2
圖2相關定理及套用
布利安桑定理(Brianchon定理) 對於任意一個外切於非退化的二級曲線的簡單六線性,它的三對對頂點的連線通過一個點(如圖3)這個點稱為布利安桑點。
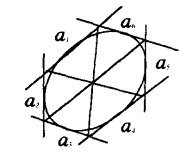 圖3
圖3以下定理為布利安桑定理的特殊情況:
定理1 外切於一條非退化二級曲線的簡單四線形,二對對頂的連線,及其對邊切點的連線,四線必共點(如圖4(a))。
定理2 外切於一條非退化二級曲線的簡單四線形,一對對頂的連線與另一對對頂中每一頂點與其對邊切點的連線,三線共點(如圖4(b))。
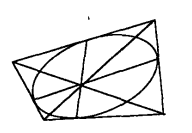 圖4(a)
圖4(a) 圖4(b)
圖4(b)例題1 已知梯形ABCD外切橢圓於G、H、Q、R,證明梯形的上下底AD、CB分別被切點R、H所分線段之比相等,即AR:RD=CH:HB(圖5)。
證明: 由關於簡單四線形的布利安桑定理知AC、BD、RH、GQ共點S,再利用相似三角形即可證得結論,也可利用
交比證明如下:
例題2 求證:雙曲線上任一點處的切線與兩漸近線所圍成的三角形的面積為常量。
證明: 如圖5,設雙曲線的兩條切線依次交兩漸近線於A,B和A’,B',於是,兩切線與兩漸近線構成雙曲線的一個外切四線形,據定理1(外切於非退化二次曲線的簡單四線形的兩雙對頂的連線及兩雙對邊上切點的連線必四線共點)可知,
共點。即
。從而三角形
與
等積,於是,三角形ABC與
等積。
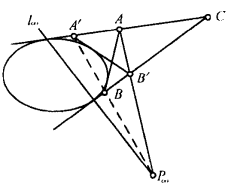 圖5
圖5相關概念
簡單n線形 n條直線(其中無三線共點)及其兩兩順次相交的交點所構成的圖形,這n條直線稱為邊,n個交點稱為頂點。
簡單n點形n個點(其中無三點共線)及其兩兩順次連線所構成的圖形,這n個點稱為頂點,n條直線稱為邊。
對於簡單n點(線)形,表1和表2分別給出了n=3和n=4的情形,顯然,對於給定的n個點(或n條直線),由它們所構成的簡單n點形(簡單n線形)與這n個點(n條直線)的排序有關。此外,這兩類圖形與初等幾何中的多邊形也是不同的概念。
 圖1
圖1 圖2
圖2 圖3
圖3 圖4(a)
圖4(a) 圖4(b)
圖4(b)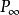







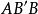

 圖5
圖5