交比亦稱非調和比。是分式線性變換的一種不變數。
在分式線性變換下任意四點的交比不變,換句話說,交比是線性變換的不變數。
基本介紹
- 中文名:交比
- 外文名:cross ratio
- 定義:基本的射影不變數之一
- 學科:射影幾何學
- 發現時間:古希臘
- 又稱:調和比
簡介


推廣

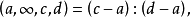
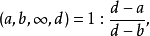

交比亦稱非調和比。是分式線性變換的一種不變數。
在分式線性變換下任意四點的交比不變,換句話說,交比是線性變換的不變數。



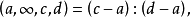
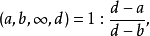

交比亦稱非調和比。是分式線性變換的一種不變數。在分式線性變換下任意四點的交比不變,換句話說,交比是線性變換的不變數。...
交比定理編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!點A,B,C,D是同一直線上依序四點,P是直線外一點,則有...
仿射變換是射影變換的特殊情況,當定義中心射影的線束為互相平行的直線時,變換稱為仿射變換,由於線束中的直線互相平行,顯然,仿射變換保持交比不變。[2] ...
指圖形經過任何射影對應(變換)都不變的量。射影不變數也是一種射影性質。例如,交比就是最基本的射影不變數,同時也是最重要的射影性質。...
當共線四點的交比B(y,s;u,v)=-1時,稱v是y、s和u的第四調和點,y、s、u、v稱為調和點列,又稱u、v調和分割y和s,或u、v和y、s調和共軛,如果平面...
兩點列l(x)到l′(x′)的點之間的一個一一對應,使l上任意4點的交比與l′上對應4點的交比相等,則此一一對應稱為點列l(x)到l′(x′)的射影對應;當兩...
射影變換有兩個重要的性質:首先,射影變換使點列變點列,直線變直線,線束變線束,點和直線的結合性是射影變換的不變性;其次,射影變換下,交比不變。交比是射影...
射影幾何里許多重要的性質都是從交比性質推導出來的。[2] 如果就幾何學內容的多少來說,射影幾何學<仿射幾何學< 歐氏幾何學,這就是說歐氏幾何學的內容最豐富,...
射影對應是射影幾何中最重要的一種對應,通常指射影空間(平面、直線)之間保持共線性和共線四點的交比不變的點的一一對應。當兩個對應的射影空間(平面、直線)...
相交於一點的4條共面線束和4個共線點對偶,因此,共點的4條共面線束也有交比不變數。對於5條共面線存在兩個射影不變數:其中 是矩陣 的行列式,而 是直線的...
拉蓋爾定理(Laguerre theorem)是射影幾何的重要定理之一。設兩條非迷向直線的交角為θ,若這兩條直線與過它們交點的兩條以-i,i為斜率的迷向直線所成的交比為...
還指出射束中四條線的交比可以用頂點P處各個角的正弦來表示,並推出這個表示法的值與任何斜截線所得的四個點的交比是相同的,由此證明了交比在截影與投影下...
一維射影對應(one-dimensional projective correspondence)是透視對應的推廣,兩個一維基本形(點列或線束)間的一一對應是射影對應的充分必要條件是任何四元素的交比...
