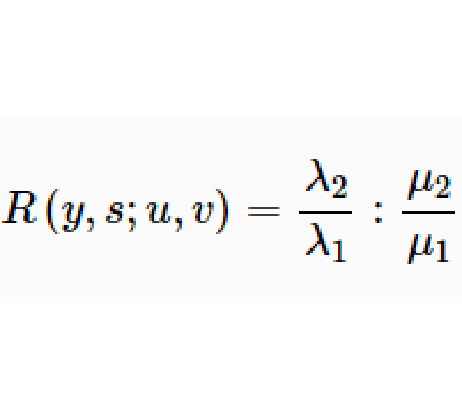調和共軛

當共線四點的交比B(y，s；u，v)=-1時，稱v是y、s和u的第四調和點，y、s、u、v稱為調和點列，又稱u、v調和分割y和s，或u、v和y、s調和共軛，如果平面上過一點的四條直線η、ζ、φ、ψ的交比等於一1，也稱φ、ψ和η、ζ是調和共軛的。

基本介紹

• 中文名：調和共扼
• 外文名：harmonic range of points
• 所屬學科：數學
• 所屬問題：高等幾何(射影幾何)
• 相關概念：射影幾何、交比等

定義

調和共扼是高等幾何中的一個重要概念，它既能體現點與點，線與線，點與線之間的一些特殊位置關係，又能對歐氏幾何中的一些概念和性質作出射影解釋，進而理順歐氏幾何與射影幾何間的某些關係。射影幾何中的調和共扼是通過交比值來定義的。

調和點列(harmonic range of points)是射影幾何的基本概念之一，即射影直線上交比等於-1的四個點，交比 時，稱點偶P₃，P₄ 調和分離點偶P₁，P₂；或稱點偶P₁，P₂與點偶P₃，P₄調和共軛；並稱P₁，P₂，P₃，P₄四點為調和共軛點；也稱P₄為P₁，P₂，P₃的第四調和點.交比-1稱為調和比，若P₁P₂是普通線段，則也稱P₃，P₄兩點把線段P₁P₂調和分割。點偶調和分離(或點偶調和共軛)的關係是相互的，即與點偶的順序無關。當(P₁P₂，P₃P₄₎=-1時，可求得由這四點構成的其他交比的值為2或1/2，並且當四點構成的交比值為2或1/2時，可以適當改變點的順序，使其中兩點與其他兩點調和共軛。

交比

交比是射影變換的基本不變數，它和高等幾何的各部分內容密切相關。調和比是特殊的交比，它不僅具有交比的一切性質，又具有自己獨特的特點和作用。當（AB，CD）=-1 時，稱 C、D 調和分割 A、B，或點偶 C、D 與點偶 A、B 成調和共軛，D稱為 A、B、C 的第四調和點。這裡，A、B、C、D 是互異的實點，在調和共軛中，兩對對應點的關係是完全對等的。由對偶原理知，運用交比和調和共軛的概念和有關性質，可以比較簡便地解決一些初等幾何和複變函數、偏微分方程方面的問題。

交比(cross ratio)又稱“複比”，如果 是直線上的四個不同點，且 則

稱為這四點在這順序下的交比。對偶地，如果 是射影平面上共點的四條不同直線，且

則

稱為這四直線在這順序下的交比，四個共線點或四條共點直線的交比在射影變換之下是不變的。

相關定理

定理1 共線四點交比取 的充要條件是四點有兩點重合。

定理2 共線的不同四點所成的六組交比中，有相同值的充 要條件是此四點能配成調和共軛。