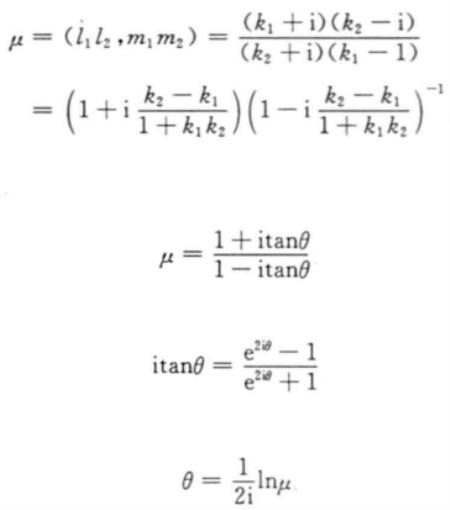拉蓋爾定理(Laguerre theorem)是射影幾何的重要定理之一。設兩條非迷向直線的交角為θ，若這兩條直線與過它們交點的兩條以-i，i為斜率的迷向直線所成的交比為μ，則θ=(ln μ)/2i，由拉蓋爾定理可得到：兩條非迷向直線垂直的充分必要條件是這兩條直線與過其交點的兩條迷向直線調和共軛，即μ=-1，亦即兩直線垂直的充分必要條件是兩直線上的無窮遠點與虛圓點調和共軛。拉蓋爾定理把交比與調和共軛這兩個射影概念表達成角與垂直這兩個度量概念，給角和垂直以射影解釋，從而把歐氏幾何與射影幾何聯繫起來。拉蓋爾(E.N.Laguerre)是最先探討復射影平面理論者之一。他建立了用交比定義角的度量公式，把歐氏幾何與射影幾何聯繫起來。
基本介紹
- 中文名：拉蓋爾定理
- 外文名：Laguerre theorem
- 簡介：射影幾何的重要定理之一
- 所屬學科：數學
- 所屬問題：高等幾何(射影幾何)
- 提出者：拉蓋爾(E.N.Laguerre)
基本介紹,拉蓋爾定理的證明,
基本介紹
之所以把I，J稱為圓點，是因為每個圓都通過這兩個點。事實上，我們有如下結論。
定理1 非退化的二階曲線是圓的充分必要條件是該二次曲線通過兩個圓點。
證明： 必要性。在齊次笛卡兒坐標系下，圓的方程是
充分性。設二階曲線
下面是重要的定理——拉蓋爾(Laguerre)定理，這個定理將兩直線的夾角與交比聯繫起來，從而為利用射影幾何知識解決歐氏幾何問題提供支持。
拉蓋爾定理 設兩條非迷向直線的夾角為
，這兩條直線與過它們交點的兩條迷向直線的交比
滿足
。
推論 兩條非迷向直線垂直的充分必要條件是這兩條直線與過它們的交點的兩條迷向直線調和共徑。
拉蓋爾定理的證明
設這兩條非迷向直線為
，過這兩條直線交點的兩條迷向直線分別為
。直線的斜率分別設為
。因為過圓點J與過圓點I的迷向直線方程分別為
(其中b,c為複數)，所以直線的斜率分別為-i，i。於是有
